
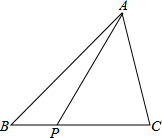
 如图,P为△ABC边BC上的一点,且PC=2a,PB=a,∠ABC=45°,∠APC=60°,则AP的长是________.
如图,P为△ABC边BC上的一点,且PC=2a,PB=a,∠ABC=45°,∠APC=60°,则AP的长是________. +1)a
+1)a PC=a,再根据等边对等角求出PD=PB=a,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BDP=∠DBP=30°,从而得到∠DBP=∠PCD,根据等角对等边可得BD=CD,根据∠ABC=45°求出∠ABD=15°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAD=15°,从而得到∠BAD=∠ABD,根据等角对等边可得AD=BD,最后根据AP=AD+PD代入数据进行计算即可得解.
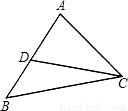
PC=a,再根据等边对等角求出PD=PB=a,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BDP=∠DBP=30°,从而得到∠DBP=∠PCD,根据等角对等边可得BD=CD,根据∠ABC=45°求出∠ABD=15°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAD=15°,从而得到∠BAD=∠ABD,根据等角对等边可得AD=BD,最后根据AP=AD+PD代入数据进行计算即可得解. 解:如图,过点C作CD⊥AP于D,
解:如图,过点C作CD⊥AP于D, PC=a,
PC=a,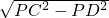 =
=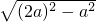 =
= a,
a, a,
a, a+a=(
a+a=( +1)a.
+1)a. +1)a.
+1)a.

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源:2006年湖北省鄂州市中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com