
分析 (1)先求出x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$,再利用x13x2+x1x23=x1x2(x12+x22)=x1x2[(x1+x2)2-2x1•x2]求解即可,
(2)先求出x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$,再利用2x12+x1x2-2x22=2(x1+x2)(x1-x2)+x1•x2=2(x1+x2)(x1-x2)+x1•x2求解即可.
解答 解:(1)∵x1,x2是方程2x2+3x-1=0的两根,
∴x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$,
∴x13x2+x1x23=x1x2(x12+x22)=x1x2[(x1+x2)2-2x1•x2]=-$\frac{1}{2}$×$\frac{13}{4}$=-$\frac{13}{8}$;
(2)∵x1,x2是方程2x2+3x-1=0的两根,
∴x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$,
∴(x1-x2)2=(x1+x2)2-4x1•x2=$\frac{9}{4}$+2=$\frac{17}{4}$,
∴x1-x2=±$\frac{\sqrt{17}}{2}$,
∴2x12+x1x2-2x22=2(x1+x2)(x1-x2)+x1•x2=2(x1+x2)(x1-x2)+x1•x2=2×(-$\frac{3}{2}$)(x1-x2)-$\frac{1}{2}$=-3(x1-x2)-$\frac{1}{2}$=±$\frac{3\sqrt{17}}{2}$-$\frac{1}{2}$.
∴2x12+x1x2-2x22=$\frac{3\sqrt{17}}{2}$-$\frac{1}{2}$或-$\frac{3\sqrt{17}}{2}$-$\frac{1}{2}$.
点评 本题主要考查了根与系数的关系,解题的关键是熟记x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{a}{b}$,x1x2=$\frac{c}{a}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3xy2)2=6xy4 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | x7÷x5=x2 | D. | (a+1)2=a2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
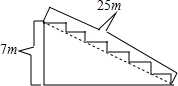 如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.| A. | 21 | B. | 75 | C. | 93 | D. | 96 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
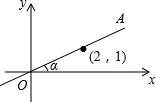 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
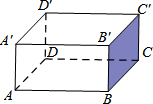 如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )
如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )| A. | $\sqrt{53}$cm | B. | $\sqrt{45}$cm | C. | $\sqrt{41}$cm | D. | 7cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com