Question

【题目】如图，E、F是ABCD对角线AC上两点，且AE=CF．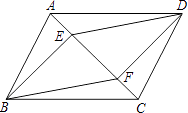
（1）求证：四边形BFDE是平行四边形．
（2）如果把条件AE=CF改为BE⊥AC，DF⊥AC，试问四边形BFDE是平行四边形吗？为什么？
（3）如果把条件AE=CF改为BE=DF，试问四边形BFDE还是平行四边形吗？为什么？

Answer 1

【答案】
（1）证明：证法一：∵ABCD是平行四边形

∴AB=CD 且AB∥CD（平行四边形的对边平行且相等）

∴∠BAE=∠DCF

又∵AE=CF

∴△BAE≌△DCF（SAS）

∴BE=DF，∠AEB=∠CFD

∴∠BEF=180°﹣∠AEB∠DFE=180°﹣∠CFD

即：∠BEF=∠DFE

∴BE∥DF，而BE=DF

∴四边形BFDE是平行四边形（一组对边平行且相等的四边形是平行四边形）

证法二：连接BD，交AC于点O．

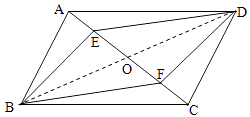
∵ABCD是平行四边形

∴OA=OC OB=OD（平行四边形的对角线互相平分）

又∵AE=CF

∴OA﹣AE=OC﹣CF，即OE=OF

∴四边形BFDE是平行四边形（对角线互相平分的四边形是平行四边形）

（2）解：四边形BFDE是平行四边形

∵ABCD是平行四边形

∴AB=CD 且AB∥CD（平行四边形的对边平行且相等）

∴∠BAE=∠DCF

∵BE⊥AC，DF⊥AC

∴∠BEA=∠DFC=90°，BE∥DF

∴△BAE≌△DCF（AAS）

∴BE=DF

∴四边形BFDE是平行四边形（一组对边平行且相等的四边形是平行四边形）

（3）解：四边形BFDE不是平行四边形

因为把条件AE=CF改为BE=DF后，不能证明△BAE与△DCF全等

【解析】（1）方法一：证明△BAE≌△DCF，推出BE=DF，BE∥DF即可．方法二：连接BD，交AC于点O．只要证明OE=OF，OB=OD即可；（2）是平行四边形．只要证明△BAE≌△DCF即可解决问题；（3）四边形BFDE不是平行四边形．因为把条件AE=CF改为BE=DF后，不能证明△BAE与△DCF全等；
【考点精析】根据题目的已知条件，利用平行四边形的判定与性质的相关知识可以得到问题的答案，需要掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．