
分析 分两种情况:①△ABC是锐角三角形时,作AD⊥BC于D,则∠ADB=90°,由已知条件得出BD=2AD,设AD=x,BD=2x,则CD=BC-BD=$\sqrt{10}$-2x,由勾股定理得出方程,解方程求出AD,即可求出结果;
②△ABC是钝角三角形时,作AD⊥BC于D,则∠ADB=90°,同①得出设AD=x,BD=2x,则CD=BC-BD=2x-$\sqrt{10}$,由勾股定理得出方程,解方程求出AD,即可求出结果;.
解答 解:分两种情况:①△ABC是锐角三角形时,如图1所示: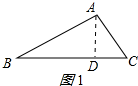
作AD⊥BC于D,则∠ADB=90°,
在Rt△ABD中,∵tanB=$\frac{AD}{BD}$=$\frac{1}{2}$,
∴BD=2AD,
∴设AD=x千米,BD=2x千米,
则CD=BC-BD=$\sqrt{10}$-2x(千米),
由勾股定理得:AD2+CD2=AC2,
即x2+($\sqrt{10}$-2x)=($\sqrt{5}$)2,
解得:x=$\frac{2\sqrt{10}-\sqrt{15}}{5}$,或$\frac{2\sqrt{10}+\sqrt{15}}{5}$,(不合题意,舍去);
∴AD=$\frac{2\sqrt{10}-\sqrt{15}}{5}$(千米),
∴这块菜地的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×$\sqrt{10}$×$\frac{2\sqrt{10}-\sqrt{15}}{5}$=$\frac{4-\sqrt{6}}{2}$(平方千米);
②△ABC是钝角三角形时,如图2所示:
作AD⊥BC于D,则∠ADB=90°,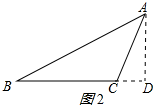
在Rt△ABD中,∵tanB=$\frac{AD}{BD}$=$\frac{1}{2}$,
∴BD=2AD,
∴设AD=x千米,BD=2x千米,
则CD=BC-BD=2x-$\sqrt{10}$(千米),
由勾股定理得:AD2+CD2=AC2,
即x2+($\sqrt{10}$-2x)=($\sqrt{5}$)2,
解得:x=$\frac{2\sqrt{10}-\sqrt{15}}{5}$(不合题意,舍去),或$\frac{2\sqrt{10}+\sqrt{15}}{5}$;
∴AD=$\frac{2\sqrt{10}+\sqrt{15}}{5}$(千米),
∴这块菜地的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×$\sqrt{10}$×$\frac{2\sqrt{10}+\sqrt{15}}{5}$=$\frac{4+\sqrt{6}}{2}$(平方千米);
综上所述:这块菜地的面积为$\frac{4±\sqrt{6}}{2}$平方千米.
点评 本题考查了解直角三角形的应用、勾股定理、解方程;熟练掌握解直角三角形,由勾股定理得出方程是解决问题的关键;注意分类讨论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com