
 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.分析 (1)首先连接OC,由OC=OA,$\widehat{BC}$=$\widehat{FC}$,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;
(2)首先证明ACE=∠ABC,由tan∠CBA=tan∠ACE=2=$\frac{AE}{EC}$,AE=4,推出EC=2,根据EC2=EF•EA,求出EF即可解决问题.
解答 (1)证明:连接OC,
∵OC=OA,
∴∠BAC=∠OCA,
∵$\widehat{BC}$=$\widehat{FC}$,
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE,
∵DE切⊙O于点C,
∴OC⊥DE.
∴AE⊥DE;
(2)解:连接CF.
∵$\widehat{BC}$=$\widehat{FC}$,
∴∠CAB=∠CAE,
∵∠CAB+∠ABC=90°,∠ACE+∠ACE=90°,
∴∠ACE=∠ABC,
∵tan∠CBA=tan∠ACE=2=$\frac{AE}{EC}$,
∵AE=4,
∴EC=2,
∵EC2=EF•EA,
∴22=EF•4,
∴EF=1,
∴AF=AE-EF=3.
点评 此题考查了切线的性质、直角三角形的性质、圆周角定理、切割线定理、锐角三角函数、平行线的性质等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.88×102 | B. | 28.8×103 | C. | 2.88×104 | D. | 0.288×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
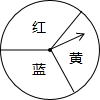 如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )
如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )| A. | 掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面 | |
| B. | 掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面 | |
| C. | 掷一枚质地均匀的骰子,奇数点朝上代表正面,偶数点朝上代表反面 | |
| D. | 转动如图所示的转盘,指针指向“红”代表正面,指针指向“蓝”代表反面 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
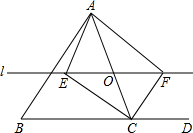 如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.
如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com