已知四条直线y=kx-3，y=-1，y=3和x=1所围成的四边形的面积是12，则k的值为（ ）
A．1或2
B．1或-2
C．-1或2
D．-1或-2
【答案】
分析：首先根据四条直线的解析式画出示意图，从而发现四边形是梯形，求得梯形的四个顶点的坐标，再进一步根据梯形的面积公式进行计算．
解答：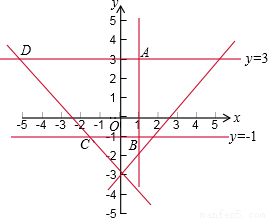
解：如图所示，根据题意，得
A（1，3），B（1，-1），C（
，-1），D（
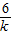
，3）．
显然ABCD是梯形，且梯形的高是4，根据梯形的面积是12，则梯形的上下底的和是6，则有
①当k＜0时，1-
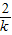
+1-
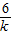
=6，
∴2-
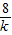
=6，
∴
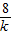
=-4，
解得k=-2；
②当k＞0时，
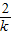
-1+
-1=6，
∴
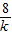
=8，
解得k=1．
综上所述，则k=-2或1．
故选B．
点评：此题考查了用图象法表示函数、两条直线的交点坐标和梯形的面积公式，注意此题的两种情况．
