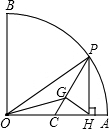
解:(1)当然是GH不变,
重心是三角形中线交点,它把中线分为1:2的比例,
如果中线长度不变,题中的三线段长度也不变,
PO是半径,它是直角三角形OPH的斜边,它的中线等于它的一半;
则GH=

(

OP)=

(

×6)=2;
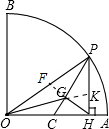
(2)延长OG交PH于点K,延长HG交OP于点F,
∵△PGH为Rt△,FG=

GH=1,PF=

OP=3,
∴PG=2

,
∴PH=
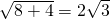
,
∴KG=

∴OG=

∴OG:PG:HG=

:2

:2=

:

:1;
(3)△PGH是等腰三角形有3种可能性,
①当GP=PH时,PH=

,
②当GP=GH时,PH=0(不存在),
③当PH=GH时,PH=2,
∴PH=

或PH=2.
分析:(1)由题意可知:重心是三角形中线交点,它把中线分为1:2的比例,如果中线长度不变,题中的三线段长度也不变.在直角三角形OHP中PO是直角三角形OPH的斜边,也是半径是保持不变的所以线段GH保持不变;则根据直角三角形中斜边的中线是斜边的一半可以求得OP中线的长度,进而求得GH的长度;
(2)延长PG交OA于C,则y=

×PC;分别再直角三角形OPh和直角三角形PHC中运用两次勾股定理即可以求出y关于x的函数解析式;
(3)分别讨论GH=PG,GH=PH,PH=PG这三种情况,根据(2)中的解析式可以分别求得x的值.
点评:本题主要考查了重心的概念以及直角三角形与等腰三角形的性质,综合性比较强,难度较大.

 上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心
上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心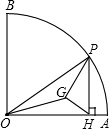 为G.
为G. 上运动时,线段GO、GP、GH中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度;
上运动时,线段GO、GP、GH中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度; 解:(1)当然是GH不变,
解:(1)当然是GH不变, (
( OP)=
OP)= (
(  ×6)=2;
×6)=2; (2)延长OG交PH于点K,延长HG交OP于点F,
(2)延长OG交PH于点K,延长HG交OP于点F, GH=1,PF=
GH=1,PF= OP=3,
OP=3, ,
,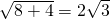 ,
, ∴OG=
∴OG=
 :2
:2 :2=
:2= :
: :1;
:1; ,
, 或PH=2.
或PH=2. ×PC;分别再直角三角形OPh和直角三角形PHC中运用两次勾股定理即可以求出y关于x的函数解析式;
×PC;分别再直角三角形OPh和直角三角形PHC中运用两次勾股定理即可以求出y关于x的函数解析式;

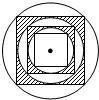 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( ) 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是