
 如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0,③b2-4ac>0,④ac>0.其中正确结论的序号为②③.(把你认为正确结论的序号都填上)
如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0,③b2-4ac>0,④ac>0.其中正确结论的序号为②③.(把你认为正确结论的序号都填上) 分析 令x=1代入可判断①;由对称轴表达式的范围可判断②;由图象与x轴有两个交点可判断③;由开口方向及与x轴的交点可分别得出a、c的符号,可判断④.
解答 解:由图象可知当x=1时,y<0,
∴a+b+c<0,
故①不正确;
由图象可知0<-$\frac{b}{2a}$<1,
∴$\frac{b}{2a}$>-1,
又∵开口向上,
∴a>0,
∴b>-2a,
∴2a+b>0,
故②正确;
由图象可知二次函数与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴△>0,即b2-4ac>0,
故③正确;
由图象可知抛物线开口向上,与y轴的交点在x轴的下方,
∴a>0,c<0,
∴ac<0,
故④不正确;
综上可知正确的为②③,
故答案为:②③.
点评 本题主要考查二次函数的图象和性质,掌握二次函数的开口方向、对称轴、与x轴的交点等知识是解题的关键.


科目:初中数学 来源: 题型:填空题
 己知,如图,在△ABC中,∠C=90°,∠A=24°,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹),直线CD即为所求.
己知,如图,在△ABC中,∠C=90°,∠A=24°,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹),直线CD即为所求.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
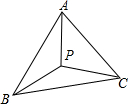 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )| A. | 110° | B. | 130° | C. | 120° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,且AD⊥BC,则∠B的度数为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,且AD⊥BC,则∠B的度数为( )| A. | 15° | B. | 25° | C. | 35° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,BC=2$\sqrt{3}$,∠CAB=30°,E,F分别是AB,CD上的点,且BE=DF=2,连结AF、CE.点P是线段AE上的点,过点P作PH∥CE交AC于点H,设AP=x.
如图,矩形ABCD中,BC=2$\sqrt{3}$,∠CAB=30°,E,F分别是AB,CD上的点,且BE=DF=2,连结AF、CE.点P是线段AE上的点,过点P作PH∥CE交AC于点H,设AP=x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com