
分析 根据一元二次方程的解的定义得到a2-5a+2=0,方程两边除以a变形得a+$\frac{2}{a}$=5,两边平方可得到a2+$\frac{4}{{a}^{2}}$=21,然后把此等式两边平方,变形后即可得到a4+16a-4.
解答 解:∵a是方程x2-5x+2=0的一个根,
∴a2-5a+2=0,
而a≠0,
∴a-5+$\frac{2}{a}$=0,即a+$\frac{2}{a}$=5,
∴(a+$\frac{2}{a}$)2=25,即a2+$\frac{4}{{a}^{2}}$=21,
∴(a2+$\frac{4}{{a}^{2}}$)2=212,
∴a4+$\frac{16}{{a}^{4}}$=433,
即a4+16a-4=433.
故答案为433.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.灵活运用完全平方公式是解决本题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 7.6×108 | B. | 0.76×10-9 | C. | 7.6×10-8 | D. | 0.76×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
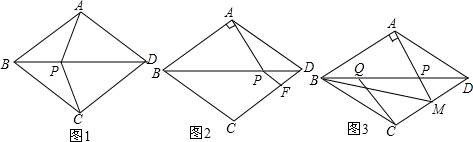 如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,
如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
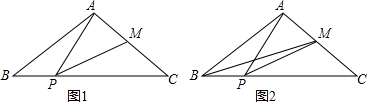 如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.
如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{BC}{AB}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{BC}{AC}$ | D. | $\frac{AB}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.
已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
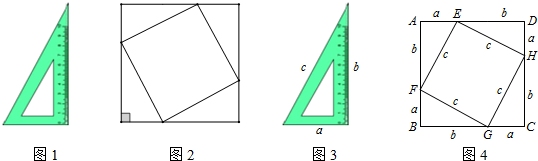
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com