



 CD,AE⊥CD,
CD,AE⊥CD, =
= =
= ,
, =
= ,
,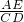 =
= =
= ,∠EAB=∠DCB,
,∠EAB=∠DCB, CD,
CD, =
= ,根据∠DBE=∠ABC=90°,∠ABE=∠DBC,得出△AEB∽△CDB,
,根据∠DBE=∠ABC=90°,∠ABE=∠DBC,得出△AEB∽△CDB,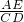 =
= =
= ,∠EAB=∠DCB,AE=
,∠EAB=∠DCB,AE= CD,再根据k>1,得出AE≠CD,最后根据∠DCB+∠COB=90°,∠AOK=∠COB,得出∠KAO+∠AOK=90°,∠AKC=90°,即可证出AE⊥CD.
CD,再根据k>1,得出AE≠CD,最后根据∠DCB+∠COB=90°,∠AOK=∠COB,得出∠KAO+∠AOK=90°,∠AKC=90°,即可证出AE⊥CD.

科目:初中数学 来源: 题型:阅读理解

|
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2013年河北省保定市中考数学一模试卷(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com