
分析 (1)先将方程变形为(x+1)2=$\frac{9}{4}$,再利用直接开平方法解方程;
(2)利用因式分解法解方程;
(3)先将方程化为一般形式,再利用因式分解法解方程;
(4)利用公式法法解方程.
解答 解:(1)2(x+1)2=4.5,
(x+1)2=$\frac{9}{4}$,
x+1=±$\frac{3}{2}$,
x+1=$\frac{3}{2}$,或x+1=-$\frac{3}{2}$,
x1=$\frac{1}{2}$,x2=-$\frac{5}{2}$;
(2)x2+2x-288=0,
(x+18)(x-16)=0,
x+18=0,或x-16=0,
x1=-18,x2=16;
(3)$\sqrt{3}$x2=5x,
$\sqrt{3}$x2-5x=0,
x($\sqrt{3}$x-5)=0,
x=0,或$\sqrt{3}$x-5=0,
x1=0,x2=$\frac{5\sqrt{3}}{3}$;
(4)4x2+3x-2=0,
∵△=9+4×4×(-2)=41,
∴x=$\frac{-3±\sqrt{41}}{8}$,
∴x1=$\frac{-3+\sqrt{41}}{8}$,x2=$\frac{-3-\sqrt{41}}{8}$.
点评 本题考查了一元二次方程的解法,能够根据题目特点灵活采取方法是解题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}{x^6}{y^3}$ | B. | $\frac{1}{4}{x^4}{y^2}$ | C. | $-\frac{1}{8}{x^6}{y^3}$ | D. | $-\frac{1}{8}{x^5}{y^3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
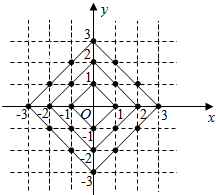 在平面直角坐标系中,横坐标、纵坐标都是整数的点称为整点,观察图中 每一个正方形(实线)四条边上的整点的个数,请你猜测出里向外第2016个正方形(实线)四条边上的整点个数共有8064个.
在平面直角坐标系中,横坐标、纵坐标都是整数的点称为整点,观察图中 每一个正方形(实线)四条边上的整点的个数,请你猜测出里向外第2016个正方形(实线)四条边上的整点个数共有8064个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的圆P周长为1.点M从A开始沿圆P按逆时针方向匀速转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{4}$变化到$\frac{2}{3}$时,求点N相应移动的路径长.
如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的圆P周长为1.点M从A开始沿圆P按逆时针方向匀速转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{4}$变化到$\frac{2}{3}$时,求点N相应移动的路径长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
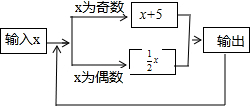 如图所示的程序计算,若开始输入的x值为12,我们发现第一次得到的结果为6,第2次得到的结果为3,…,请你探索第2010次得到的结果为1.
如图所示的程序计算,若开始输入的x值为12,我们发现第一次得到的结果为6,第2次得到的结果为3,…,请你探索第2010次得到的结果为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com