
科目:初中数学 来源: 题型:填空题
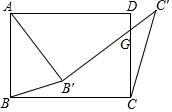 如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则$\frac{CC'}{{{B}{B}'}}$=$\frac{\sqrt{74}}{5}$(结果保留根号).
如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则$\frac{CC'}{{{B}{B}'}}$=$\frac{\sqrt{74}}{5}$(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
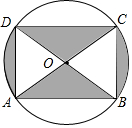 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )| A. | 5πcm2 | B. | 10πcm2 | C. | 15πcm2 | D. | 20πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
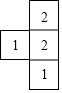 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数,则该几何体的左视图是( )
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数,则该几何体的左视图是( )| A. | 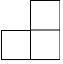 | B. | 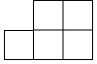 | C. | 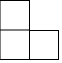 | D. | 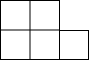 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 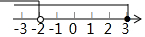 | B. |  | ||
| C. | 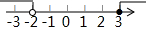 | D. | 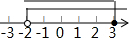 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
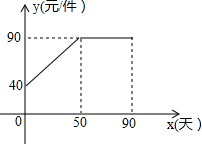 九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如图,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元).
九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如图,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元).| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量 p(件) | 198 | 140 | 80 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com