考点:二次函数图象上点的坐标特征,等边三角形的性质
专题:规律型
分析:根据等边三角形的性质可得∠A1A0B1=60°,然后表示出A0B1的解析式,与二次函数解析式联立求出点B1的坐标,再根据等边三角形的性质求出A0A1,同理表示出A1B2的解析式,与二次函数解析式联立求出点B2的坐标,再根据等边三角形的性质求出A1A2,同理求出B3的坐标,然后求出A2A3,从而得到等边三角形的边长为从1开始的连续自然数,与三角形所在的序数相等.
解答:解:∵△A
0B
1A
1是等边三角形,
∴∠A
1A
0B
1=60°,
∴A
0B
1的解析式为y=
x,
联立
,
解得
,
(为原点,舍去),
∴点B
1(
,
),
∴等边△A
0B
1A
1的边长为
×2=1,
同理,A
1B
2的解析式为y=
x+1,
联立
,
解得
,
(在第二象限,舍去),
∴B
2(
,2),
∴等边△A
1B
2A
2的边长A
1A
2=2×(2-1)=2,
同理可求出B
3(
,
),
所以,等边△A
2B
3A
3的边长A
2A
3=2×(
-1-2)=3,
…,
以此类推,系列等边三角形的边长为从1开始的连续自然数,
△A
2014B
2015A
2015的边长A
2014A
2015=2015.
故答案为:2015.
点评:本题考查了二次函数图象上点的坐标特征,等边三角形的性质,主要利用了联立两函数解析式求交点坐标,根据点B系列的坐标求出等边三角形的边长并且发现系列等边三角形的边长为从1开始的连续自然数是解题的关键.

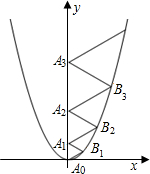 二次函数y=
二次函数y=

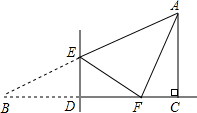 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=9.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=9.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为