
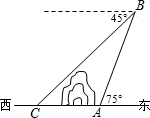
 如图,在小山的东侧A处有一热气球,以每分钟10米的速度沿着仰角为75°的方向上升,20分钟后上升到B处,这时气球上的人发现在点A的正西方向俯角为45°的C处有一着火点,求气球的升空点A与着火点C之间的距离.(结果保留根号)
如图,在小山的东侧A处有一热气球,以每分钟10米的速度沿着仰角为75°的方向上升,20分钟后上升到B处,这时气球上的人发现在点A的正西方向俯角为45°的C处有一着火点,求气球的升空点A与着火点C之间的距离.(结果保留根号)
| 1 |
| 2 |
| AD |
| sin45° |
| 100 | ||||
|
| 2 |
| 2 |


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
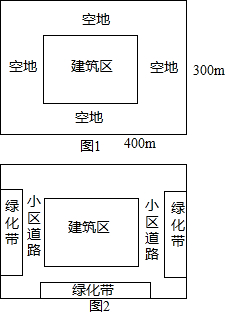 如图1,某小区的平面图是一个占地400×300平方米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%,南北空地等宽,东西空地等宽.
如图1,某小区的平面图是一个占地400×300平方米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%,南北空地等宽,东西空地等宽.查看答案和解析>>
科目:初中数学 来源: 题型:
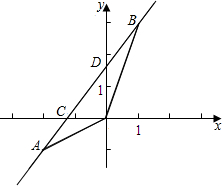 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com