
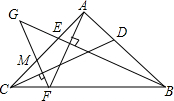
 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.以下五个结论:①△ADC≌△AEB;②∠AEG=∠CDB;③△EGM是等腰三角形;④BG=AF+FG;恒成立的结论有①②③④.(把你认为正确的序号都填上)
如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.以下五个结论:①△ADC≌△AEB;②∠AEG=∠CDB;③△EGM是等腰三角形;④BG=AF+FG;恒成立的结论有①②③④.(把你认为正确的序号都填上) 分析 ①首先得出AC=AB,再利用SAS,得出△ACD≌△ABE即可;
②③利用△ACD≌△ABE,得出∠1=∠3,再由∠BAC=90°,可得∠3+∠2=90°,结合FG⊥CD可得出∠3=∠CMF,∠GEM=∠GME,继而可得出结论;
④先大致观察三者的关系,过点B作AB的垂线,交GF的延长线于点N,利用(1)的结论可将AF转化为NF,BG转化为NG,从而在一条直线上得出三者的关系.
解答 解:等腰直角三角形ABC中,∠BAC=90°,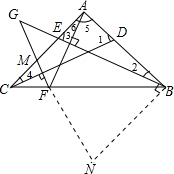 ∴AC=AB,∠ACB=∠ABC=45°,
∴AC=AB,∠ACB=∠ABC=45°,
在△ADC和△AEB中,
$\left\{\begin{array}{l}{AC=AB\\;}\\{∠CAD=∠BAE}\\{AD=AE}\end{array}\right.$,
∴△ADC≌△AEB(SAS),故①正确;
∵ADC≌△AEB,
∴∠1=∠3,故②∠AEG=∠CDB正确;
∵∠BAC=90°,
∴∠3+∠2=90°,∠1+∠4=90°,
∴∠4+∠3=90°
∵FG⊥CD,
∴∠CMF+∠4=90°,
∴∠3=∠CMF,
∴∠GEM=∠GME,
∴EG=MG,△EGM为等腰三角形,故③正确;
过点B作AB的垂线,交GF的延长线于点N,
∵BN⊥AB,∠ABC=45°,
∴∠FBN=45°=∠FBA.
∵FG⊥CD,
∴∠BFN=∠CFM=90°-∠DCB,
∵AF⊥BE,
∴∠BFA=90°-∠EBC,∠5+∠2=90°,
由①可得∠DCB=∠EBC,
∴∠BFN=∠BFA,
在△BFN和△BFA中,
$\left\{\begin{array}{l}{∠FBN=∠FBA}\\{BF=BF}\\{∠BFN=∠BFA}\end{array}\right.$,
∴△BFN≌△BFA(ASA),
∴NF=AF,∠N=∠5,
又∵∠GBN+∠2=90°,
∴∠GBN=∠5=∠N,
∴BG=NG,
又∵NG=NF+FG,
∴BG=AF+FG,故④正确;
故答案为:①②③④.
点评 本题考查了全等三角形的判定及性质,难度较大,尤其是第3问的证明,要学会要判断三条线段之间的关系,一般都需要转化到同一条直线上进行.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{15}$ | B. | -$\sqrt{6}$ | C. | $\sqrt{8}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.
如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
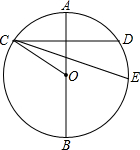 如图,AB为⊙O的一条固定直径,自左半圆上一点C,作弦CD⊥AB,∠OCD的平分线交⊙O于点E,当点C在左半圆(不包括A,B两点)上移动时,关于点E的说法:
如图,AB为⊙O的一条固定直径,自左半圆上一点C,作弦CD⊥AB,∠OCD的平分线交⊙O于点E,当点C在左半圆(不包括A,B两点)上移动时,关于点E的说法:| A. | ①② | B. | ②③ | C. | ② | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9(x-40)+50=6x | B. | 9(x-40)-50=6x | C. | $\frac{x+50}{9}$+40=$\frac{x}{6}$ | D. | $\frac{x+50}{9}$-40=$\frac{x}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com