
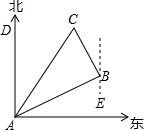 如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500
如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500 米到达B点,然后再沿北偏西30°方向走了500米到达目的地C点.
米到达B点,然后再沿北偏西30°方向走了500米到达目的地C点.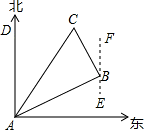
 ,BC=500,由勾股定理得:
,BC=500,由勾股定理得: =1000,
=1000,

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:单选题
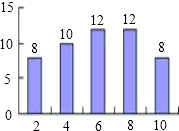 老师布置10道作业题,学习委员将全班同学的答题情况绘制成条形图,根据统计图可知,答对8道题以上的同学占全班同学的百分数是
老师布置10道作业题,学习委员将全班同学的答题情况绘制成条形图,根据统计图可知,答对8道题以上的同学占全班同学的百分数是查看答案和解析>>
科目:初中数学 来源: 题型:单选题
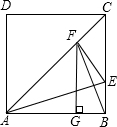 已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.下列结论①BF⊥AC,②CE2=2BE2,③AB2=2FG2.其中正确的是
已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.下列结论①BF⊥AC,②CE2=2BE2,③AB2=2FG2.其中正确的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com