
 m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积大约是( )(精确到0.1m2)
m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积大约是( )(精确到0.1m2)
 ,由此利用勾股定理求出BD=20,又∵cos∠ADB=
,由此利用勾股定理求出BD=20,又∵cos∠ADB= =
= ,∴∠ADB=60°,又矩形对角线互相平分且相等,便道的宽为1m,所以每个扇环都是圆心角为30°且外环半径为10.5,内环半径为9.5.这样可以求出每个扇环的面积.
,∴∠ADB=60°,又矩形对角线互相平分且相等,便道的宽为1m,所以每个扇环都是圆心角为30°且外环半径为10.5,内环半径为9.5.这样可以求出每个扇环的面积. 解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形, ,
, =20,
=20, =
= ,
, =
= .
.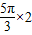 =10.4666≈10.5m2.
=10.4666≈10.5m2.

 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源:2006年广东省佛山市中考数学试卷(课标卷)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年广东省佛山市中考数学试卷(课标卷)(解析版) 题型:选择题
 m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积大约是( )(精确到0.1m2)
m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积大约是( )(精确到0.1m2)
查看答案和解析>>
科目:初中数学 来源:2006年广东省佛山市中考数学试卷(课标卷)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2006年广东省佛山市中考数学试卷(课标卷)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com