
 如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;
如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由AB的垂直平分线DE交AC于D,交AB于E,可得AD=BD,即可求得∠ABD=∠A=36°,又由AB=AC,即可求得∠CBD=∠ABD=36°,∠BDC=∠C=72°,继而证得AD=BD=BC,△BDC的周长等于AB+BC.
解答 解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠CBD=∠ABD=36°,
即BD平分∠ABC;故①正确;
∴∠BDC=∠C=72°,
∴BC=BD,
∴BC=BD=AD,故②正确;
∴△BDC的周长为:BC+CD+BD=BC+C+AD=AC+BC=AB+BC;故③正确;
∵∠A=∠ABD=36°,
∴∠ADE=∠BDE=54°,
∴AE≠DE.故④错误.
故选C.
点评 本题考查了线段垂直平分线的性质以及等腰三角形的性质与判定.此题难度不大,注意掌握数形结合思想的应用.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
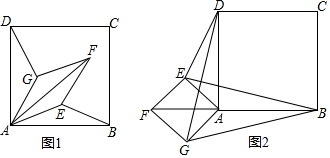
 如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则sin∠BAC的值( )
如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则sin∠BAC的值( )| A. | $\frac{6\sqrt{13}}{65}$ | B. | $\frac{5\sqrt{13}}{78}$ | C. | $\frac{\sqrt{13}}{13}$ | D. | $\frac{5\sqrt{13}}{26}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
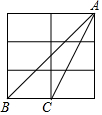
 如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,则点E与点C之间的距离是$\sqrt{5}$cm.
如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,则点E与点C之间的距离是$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两直线平行,同旁内角可能相等 | |
| B. | 同底数幂相乘,底数相乘,指数相加 | |
| C. | 一个图形和它经过平移所得的图形中,两组对应点的连线一定平行 | |
| D. | 任何数的0次幂等于1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
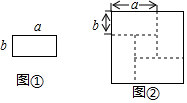 小翠利用如图①所示的长为a、宽为b的长方形卡片4张,拼成了如图②所示的图形,则根据图②的面积关系能验证的恒等式为( )
小翠利用如图①所示的长为a、宽为b的长方形卡片4张,拼成了如图②所示的图形,则根据图②的面积关系能验证的恒等式为( )| A. | (a-b)2+4ab=(a+b)2 | B. | (a-b)(a+b)=a2-b2 | C. | (a+b)2=a2+2ab+b2 | D. | (a-b)2=a2-2ab+b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com