练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．（1）计算：$\sqrt{16}$+（-$\root{3}{5}$）3-$\root{3}{64}$
    （2）已知4x2-9=0，求x的值．

    分析 （1）原式利用平方根及立方根定义计算即可得到结果；
    （2）方程整理后，利用平方根定义开方即可求出解．

    解答 解：（1）原式=4-5-4=-5；
    （2）方程整理得：x2=$\frac{9}{4}$，
    开方得：x=±$\frac{3}{2}$．

    点评 此题考查了实数的运算，以及平方根，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．中秋节期间，某商场为了吸引顾客，开展有奖促销活动，设立了一个可以自由转动的转盘，转盘被分成三个面积相等的扇形，三个扇形区域里分别标有“10元”、“20元”、“30元”的字样（如图）．规定：同一天内，顾客在本商场每消费满100元，就可以转动转盘一次，商场根据转盘指针指向区域所标金额返还相应数额的购物券．某顾客当天消费240元，转了两次转盘．
    （1）该顾客最多可得元购物券；
    （2）用画树状图或列表的方法，求该顾客所获购物券金额不低于40元的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．代数式-2x，0，3x-y，$\frac{x+y}{4}$，$\frac{x}{π}$中，单项式的个数有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

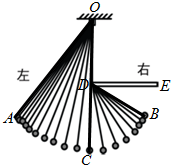    3．如图，一条细绳系着一个小球在平面内摆动．已知细绳从悬挂点O到球心的长度为50厘米，小球在A、B两个位置时达到最高点，且最高点高度相同（不计空气阻力），在C点位置时达到最低点．达到左侧最高点时与最低点时细绳相应所成的角度为37°，细绳在右侧达到最高点时与一个水平放置的挡板DE所成的角度为30°．（sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
    （1）求小球达到最高点位置与最低点位置时的高度差．
    （2）求OD这段细绳的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知二次函数y=ax2+bx+c（a≠0）的图象上部分点的横坐标x与纵坐标y的对应值如下表所示：
    x…-1024…
    y…-511m…
    求：
    （1）这个二次函数的解析式；
    （2）这个二次函数图象的顶点坐标及上表中m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列各组运算中，结果为负数的是（　　）
    A．-（-2）3B．-|-3|C．（-2）×（-4）D．（-1）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．在半径为6的⊙O中，120°圆心角所对的弧长是（　　）
    A．πB．2πC．4πD．6π

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列各数是无理数的为（　　）
    A．-5B．$\frac{π}{3}$C．4.121121112D．$\frac{22}{7}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．阅读理解．
    阅读下列材料：
    老师提倡同学们自己出题，下面是王海同学出的两道题及解答过程：
    题目1：已知（a-3）2+|b-1|=0，求a，b的值．
    解：∵（a-3）2+|b-1|=0，
    ∴a-3=0，b-1=0．
    ∴a=3，b=1．
    题目2：已知（a-3）2+|b-1|=1，求a，b的值．
    解：∵（a-3）2+|b-1|=1，
    ∴（a-3）2=0，|b-1|=1或（a-3）2=1，|b-1|=0．
    ∴a=3，b=0；a=3，b=2；a=4，b=1；a=2，b=1．
    老师说：“题目1的解答过程跳步了．题目2在编制时应该再添加已知条件”．
    请阅读以上材料，解答下列问题：
    （1）补全题目1的解答过程；
    （2）依据题目2的解答过程，题目2中应添加的已知条件是：a、b为整数．

    查看答案和解析>>

    同步练习册答案