Question

阅读下面材料：
小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB的度数．
小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决．
请你回答：图1中∠APB的度数等于______．
参考小伟同学思考问题的方法，解决下列问题：
（1）如图3，在正方形ABCD内有一点P，且PA=，PB=1，PD=，则∠APB的度数等于______，正方形的边长为______；
（2）如图4，在正六边形ABCDEF内有一点P，且PA=2，PB=1，PF=，则∠APB的度数等于______，正六边形的边长为______．

Answer 1

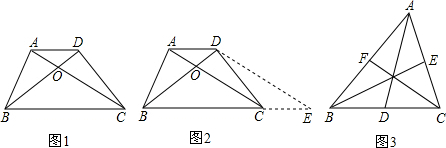
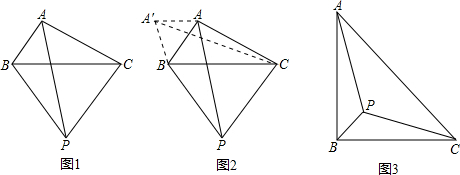
解：阅读材料：把△APB绕点A逆时针旋转60°得到△ACP′，
由旋转的性质，P′A=PA=3，P′C=PB=4，∠PAP′=60°，
∴△APP′是等边三角形，
∴PP′=PA=3，∠AP′P=60°，
∵PP′²+P′C²=3²+4²=25，PC²=5²=25，
∴PP′²+P′C²=PC²，
∴∠PP′C=90°，
∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°；
故∠APB=∠AP′C=150°；

（1）如图3，把△APB绕点A逆时针旋转90°得到△ADP′，
由旋转的性质，P′A=PA=2，P′D=PB=1，∠PAP′=90°，
∴△APP′是等腰直角三角形，
∴PP′=PA=×2=4，∠AP′P=45°，
∵PP′²+P′D²=4²+1²=17，PD²=²=17，
∴PP′²+P′D²=PD²，
∴∠PP′D=90°，
∴∠AP′D=∠AP′P+∠PP′D=45°+90°=135°，
故，∠APB=∠AP′D=135°，
∵∠APB+∠APP′=135°+45°=180°，
∴点P′、P、B三点共线，
过点A作AE⊥PP′于E，
则AE=PE=PP′=×4=2，
∴BE=PE+PB=2+1=3，
在Rt△ABE中，AB===；

（2）如图4，∵正六边形的内角为×（6-2）•180°120°，
∴把△APB绕点A逆时针旋转120°得到△AFP′，
由旋转的性质，P′A=PA=2，P′F=PB=1，∠PAP′=120°，
∴∠APP′=∠AP′P=（180°-120°）=30°，
过点A作AM⊥PP′于M，设PP′与AF相交于N，
则AM=PA=×2=1，
P′M=PM===，
∴PP′=2PM=2，
∵PP′²+P′F²=（2）²+1²=13，PF²=²=13，
∴PP′²+P′F²=PF²，
∴∠PP′F=90°，
∴∠AP′F=∠AP′P+∠PP′F=30°+90°=120°，
故，∠APB=∠AP′F=120°，
∵P′F=AM=1，
∵△AMN和△FP′N中，
，
∴△AMN≌△FP′N（AAS），
∴AN=FN，P′N=MN=P′M=，
在Rt△AMN中，AN===，
∴AF=2AN=2×=．
故答案为：150°；（1）135°，；（2）120°，．
分析：阅读材料：把△APB绕点A逆时针旋转60°得到△ACP′，根据旋转的性质可得P′A=PA，P′C=PB，∠PAP′=60°，然后求出△APP′是等边三角形，根据等边三角形的性质求出PP′=PA=3，∠AP′P=60°，再利用勾股定理逆定理求出∠PP′C=90°，然后求出∠AP′C，即为∠APB的度数；
（1）把△APB绕点A逆时针旋转90°得到△ADP′，根据旋转的性质可得P′A=PA，P′D=PB，∠PAP′=90°，然后判断出△APP′是等腰直角三角形，根据等腰直角三角形的性质求出PP′，∠AP′P=45°，再利用勾股定理逆定理求出∠PP′D=90°，然后求出∠AP′D，即为∠APB的度数；再求出点P′、P、B三点共线，过点A作AE⊥PP′于E，根据等腰直角三角形的性质求出AE=PE=PP′，然后求出BE，在Rt△ABE中，利用勾股定理列式求出AB即可；
（2）把△APB绕点A逆时针旋转120°得到△AFP′，根据旋转的性质可得P′A=PA，P′F=PB，∠PAP′=120°，然后求出△APP′是底角为30°的等腰三角形，过点A作AM⊥PP′于M，设PP′与AF相交于N，求出AM=1，再求出PP′，∠AP′P=30°，再利用勾股定理逆定理求出∠PP′F=90°，然后求出∠AP′F，即为∠APB的度数；根据P′F、AM的长度得到P′F=AM，利用“角角边”证明△AMN和△FP′N全等，根据全等三角形对应边相等可得AN=FN，P′N=MN，然后求出MN，在Rt△AMN中，利用勾股定理列式求出AN，然后求出AF即可．
点评：本题考查了旋转的性质，等边三角形的性质，正方形的性质，勾股定理以及勾股定理逆定理的应用，全等三角形的判定与性质，（1）（2）两问求多边形的边长有一定的难度，作辅助线构造出直角三角形与全等三角形是解题的关键．