
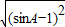 = .
= . 科目:初中数学 来源:2012年四川省资阳市中考数学模拟试卷(三)(解析版) 题型:解答题
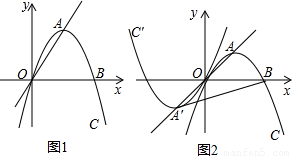
查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市中考数学模拟试卷(48)(解析版) 题型:解答题
 厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP.设运动时间为t秒(t>0).
厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP.设运动时间为t秒(t>0).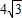 厘米.
厘米.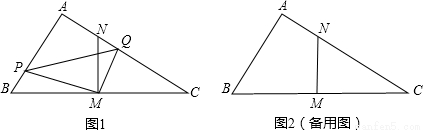
查看答案和解析>>
科目:初中数学 来源:2011年四川省资阳市中考数学试卷(解析版) 题型:解答题
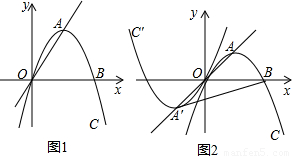
查看答案和解析>>
科目:初中数学 来源:2010年福建省福州市闽侯县实验中学中考数学模拟试卷(解析版) 题型:填空题
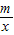 (m≠0)的交点,过点A作AC平行于x轴,过点B作BC平行于y轴,AC与y轴交于点M,BC与x轴交于点N,若∠BAC=60°,AB=4,
(m≠0)的交点,过点A作AC平行于x轴,过点B作BC平行于y轴,AC与y轴交于点M,BC与x轴交于点N,若∠BAC=60°,AB=4,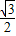 时,求点P的坐标.
时,求点P的坐标.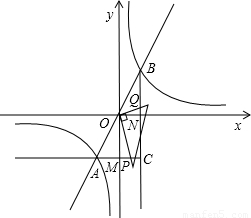
查看答案和解析>>
科目:初中数学 来源:2011年江苏省扬州市中考数学试卷(解析版) 题型:解答题
 厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ丄MP.设运动时间为t秒(t>0).
厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ丄MP.设运动时间为t秒(t>0).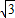 厘米.
厘米.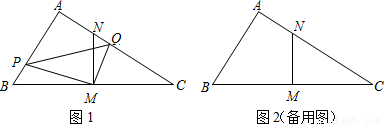
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com