


科目:初中数学 来源: 题型:
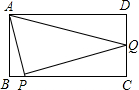 位/秒的速度沿着B→C方向运动.设从点B出发运动了x秒,
位/秒的速度沿着B→C方向运动.设从点B出发运动了x秒,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•昌平区一模)如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(2012•昌平区一模)如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).| 1 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线![]() 与
与![]() 轴交于A(-1,0)、B(3,0)两点,与
轴交于A(-1,0)、B(3,0)两点,与![]() 轴交于点C(0,3).
轴交于点C(0,3).
(1)求抛物线的解析式及顶点M坐标;
(2)在抛物线的对称轴上找到点P,使得△PAC的周长最小,并求出点P的坐标;
(3)若点D是线段OC上的一个动点(不与点O、C重合).过点D作DE∥PC交![]() 轴于点E.设CD的长为m,问当m取何值时,S△PDE =
轴于点E.设CD的长为m,问当m取何值时,S△PDE =![]() S四边形ABMC.
S四边形ABMC.

查看答案和解析>>
科目:初中数学 来源:2012年北京市昌平区中考数学一模试卷(解析版) 题型:解答题
 S四边形ABMC.
S四边形ABMC.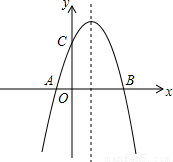
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com