Question

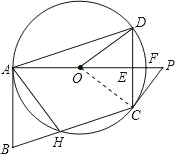
【题目】如图，⊙O过ABCD的三顶点A、D、C，边AB与⊙O相切于点A，边BC与⊙O相交于点H，射线AD交边CD于点E，交⊙O于点F，点P在射线AO上，且∠PCD=2∠DAF．

（1）求证：△ABH是等腰三角形；

（2）求证：直线PC是⊙O的切线；

（3）若AB=2，AD=，求⊙O的半径．

Answer 1

【答案】(1)证明参见解析；（2）证明参见解析；（3）．

【解析】

试题分析：（1）要想证明△ABH是等腰三角形，只需要根据平行四边形的性质可得∠B=∠ADC，再根据圆内接四边形的对角互补，可得∠ADC+∠AHC=180°，再根据邻补角互补，可知∠AHC+∠AHB=180°，从而可以得到∠ABH和∠AHB的关系，从而可以证明结论成立；（2）要证直线PC是⊙O的切线，只需要连接OC，证明∠OCP=90°即可，根据平行四边形的性质和边AB与⊙O相切于点A，可以得到∠AEC的度数，又∠PCD=2∠DAF，∠DOF=2∠DAF，∠COE=∠DOF，通过转化可以得到∠OCP的度数，从而可以证明结论；（3）根据题意和（1）（2）可以得到∠AED=90°，由平行四边形的性质和勾股定理，由AB=2，AD=，可以求得半径的长．

试题解析：（1）证明：∵四边形ADCH是圆内接四边形，∴∠ADC+∠AHC=180°，又∵∠AHC+∠AHB=180°，∴∠ADC=∠AHB，∵四边形ABCD是平行四边形，∴∠ADC=∠B，∴∠AHB=∠B，∴AB=AH，∴△ABH是等腰三角形；（2）证明：连接OC，如右图所示，∵边AB与⊙O相切于点A，∴BA⊥AF，∵四边形ABCD是平行四边形，∴AB∥CD，∴CD⊥AF，又∵FA经过圆心O，∴弧DF=弧CF，∠OEC=90°，∴∠COF=2∠DAF，又∵∠PCD=2∠DAF，∴∠COF=∠PCD，∵∠COF+∠OCE=90°，∴∠PCD+∠OCE=90°，即∠OCP=90°，

∴直线PC是⊙O的切线；（3）∵四边形ABCD是平行四边形，∴DC=AB=2，∵FA⊥CD，∴DE=CE=1，∵∠AED=90°，AD=，DE=1，∴AE=，设⊙O的半径为r，则OA=OD=r，OE=AE﹣OA=4﹣r，∵∠OED=90°，DE=1，∴r2=（4﹣r）2+12,解得，r=，即⊙O的半径是．