练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，射线OA的方向是北偏东20°，射线OB的方向是北偏西40°，OD是OB的反向延长线．若OC是∠AOD的平分线，则∠BOC=_____°，射线OC的方向是_____．

    【答案】120， 北偏东80°．

    【解析】

    先求出∠AOB=60°，再求得∠AOD的度数，由角平分线得出∠AOC的度数，得出∠BOC的度数，即可确定OC的方向．

    ∵OB的方向是北偏西40°，OA的方向是北偏东20°，∴∠AOB=40°+20°=60°，∴∠AOD=180°﹣60°=120°．

    ∵OC是∠AOD的平分线，∴∠AOC=60°，∴∠BOC=60°+60°=120°；

    ∵20°+60°=80°，∴射线OC的方向是北偏东80°．

    故答案为：120，北偏东80°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）若关于x的方程2x﹣3=1和=k﹣3x有相同的解，求k的值

    （2）阅读材料：解方程组时，可由①得x﹣y=1③，然后再将③代入②得4×1﹣y=5，求得y=﹣1，从而进一步求得，这种方法被称为“整体代入法”，请用上述方法解方程组

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式组 请结合题意填空，完成本题的解答；
    （Ⅰ）解不等式①，得；
    （Ⅱ）解不等式②，得；
    （Ⅲ）把不等式①和②的解集在数轴上表示出来：
    （Ⅳ）原不等式组的解集为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为线段上一动点，分别过点作，，连接.已知，设.

    (1)用含的代数式表示的值;

    (2)探究:当点满足什么条件时，的值最小?最小值是多少?

    (3)根据(2)中的结论，请构造图形求代数式的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

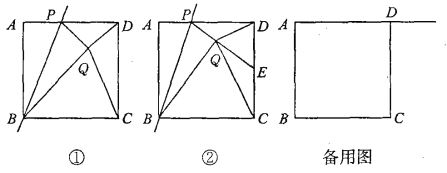
    【题目】如图①，已知正方形ABCD的边长为1，点P是AD边上的一个动点，点A关于直线BP的对称点是点Q，连接PQ、DQ、CQ、BQ，设AP＝x．

    （1）BQ＋DQ的最小值是_______，此时x的值是_______；

    （2）如图②，若PQ的延长线交CD边于点E，并且∠CQD＝90°．

    ①求证：点E是CD的中点； ②求x的值．

    （3）若点P是射线AD上的一个动点，请直接写出当△CDQ为等腰三角形时x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

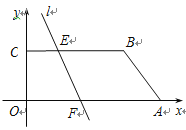
    【题目】如图，在直角坐标系中，O（0，0），A（7，0），B（5，2），C（0，2）一条动直线l分别与BC、OA交于 点E、F，且将四边形OABC分为面积相等的两部分，则点C到动直线l的距离的最大值为____,

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的少20人，现在需要从报名第二门课的人中调出10人学习第一门课，那么：

    （1）报两门课的共有多少人？

    （2）调动后，报名第一门课的人数为　 　人，第二门课人数为　 　人．

    （3）调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x的值代入，并求出具体的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E是ABCD的边CD的中点，延长AE交BC的延长线于点F．

    （1）求证：△ADE≌△FCE．

    （2）若∠BAF=90°，BC=5，EF=3，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．
    （1）设第x天生产空调y台，直接写出y与x之间的函数解析式，并写出自变量x的取值范围．
    （2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第x天的利润为W元，试求W与x之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

    查看答案和解析>>

    同步练习册答案