

分析 (1)根据题意即可得到结论;
(2)过P作PC⊥x轴于C,PD⊥y轴于D,得到四边形APBO是正方形,求得∠CPD=90°,推出△PDB≌△PAC,根据全等三角形的性质得到PB=PA,根据等腰直角三角形的判定定理即可得到结论;
(3)根据全等三角形的性质即可得到结论.
解答 解:(1)∵PA⊥x轴,点P(2,2),
∴OA=2,
∴A(2,0);
(2)过P作PC⊥x轴于C,PD⊥y轴于D,
∵OP平分∠yOx,
∴PD=PC,
∴四边形APBO是正方形,
∴∠CPD=90°,
∵∠APB=90°,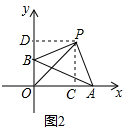
∴∠APC=∠DPB,
在△PDB与△PAC中,
$\left\{\begin{array}{l}{∠PDB=∠PCA=90°}\\{∠DPB=∠APC}\\{PD=PC}\end{array}\right.$,
∴△PDB≌△PAC,
∴PB=PA,
∵∠APB=90°,
∴△APB是等腰直角三角形;
(3)∵点P(2,2),
∴PC=PD=2,
∵△PDB≌△PAC,
∴S四边形APBO=S正方形CPDO=2×2=4.
点评 本题考查了全等三角形的判定和性质,正方形的判定和性质,等腰直角三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 乘坐高铁对旅客的行李的检查 | |
| B. | 了解全校师生对重庆一中85周年校庆文艺表演节目的满意程度 | |
| C. | 调查初2016级15班全体同学的身高情况 | |
| D. | 对新研发的新型战斗机的零部件进行检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
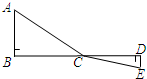 阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.
阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com