
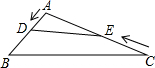
 如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为3cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是$\frac{6}{5}$秒或$\frac{12}{7}$秒.
如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为3cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是$\frac{6}{5}$秒或$\frac{12}{7}$秒. 分析 根据相似三角形的性质,由题意可知有两种相似形式,△ADE∽△ABC和△ADE∽△ACB,再由相似三角形的性质即可得出结论.
解答 解:∵AB=3cm,AC=6cm,点D运动的速度为1cm/s,点E运动的速度为3cm/s,
∴AD=t,AE=6-3t,
当△ADE∽△ABC时,$\frac{AD}{AB}$=$\frac{AE}{AC}$,即$\frac{t}{3}$=$\frac{6-3t}{6}$,解得t=$\frac{6}{5}$(秒);
当△ADE∽△ACB时,$\frac{AD}{AC}$=$\frac{AE}{AB}$,即$\frac{t}{6}$=$\frac{6-3t}{3}$,解得t=$\frac{12}{7}$(秒).
故答案为:$\frac{6}{5}$秒或$\frac{12}{7}$秒.
点评 本题考查的是相似三角形的判定与性质,在解答此题时要注意进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 △ABC和△FED中,AD=FC,∠A=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).
△ABC和△FED中,AD=FC,∠A=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在⊙O外 | B. | 在⊙O上 | C. | 在⊙O内 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=4,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=4,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com