
 如图,半径为5的⊙O中,弦AB,CD所对的圆心角分别是∠AOB,∠COD.已知CD=6,∠AOB+∠COD=180°,则弦AB的弦心距等于3.
如图,半径为5的⊙O中,弦AB,CD所对的圆心角分别是∠AOB,∠COD.已知CD=6,∠AOB+∠COD=180°,则弦AB的弦心距等于3. 分析 首先作OF⊥AB于F,作直径BE,连接AE,进而得出AE=DC,再利用三角形中位线的性质得出答案.
解答 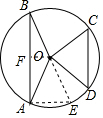 解:作OF⊥AB于F,作直径BE,连接AE,如图,
解:作OF⊥AB于F,作直径BE,连接AE,如图,
∵∠AOB+∠COD=180°,
而∠AOE+∠AOB=180°,
∴∠AOE=∠COD,
∴$\widehat{AE}$=$\widehat{DC}$,
∴AE=DC=6,
∵OF⊥AB,
∴BF=AF,
而OB=OE,
∴OF为△ABE的中位线,
∴OF=$\frac{1}{2}$AE=3.
故答案为:3.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和三角形中位线性质.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{5}$ | C. | $\frac{{18\sqrt{3}}}{13}$ | D. | $\frac{{12\sqrt{3}}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,过格点A、B、C作一圆弧.
在平面直角坐标系中,过格点A、B、C作一圆弧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/kg) | 售价(元/kg) | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:
如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com