
已知:如图,矩形ABCD,AB = 4,∠ACB = 30°.点E从点C出发,沿折线CA—AD以每秒一个单位长度的速度运动,过点E作EF∥CD交BC于点F,同时过点E作EG⊥AC交直线BC于点G,设运动的时间为t,△EFG与△ABC重叠部分的面积为S,当点E运动到点D时停止运动.
(1)当点B与点G重合时,求此时t的值;
(2)直接写出S与t之间的函数关系式和相应的自变量取值范围;
(3)当t = 4时,将△EFG绕点E顺时针旋转一个角度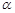 (
(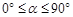 ),∠GEF的两边分别交矩形的边于点M,点N.当△MEN为等腰三角形时,求此时△MEN的面积.
),∠GEF的两边分别交矩形的边于点M,点N.当△MEN为等腰三角形时,求此时△MEN的面积.
(1)6或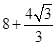 ;(2)
;(2)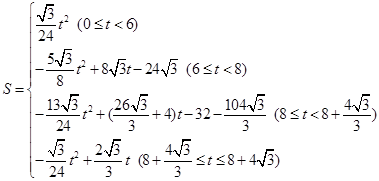 ;
;
(3)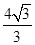 或
或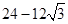 .
.
解析试题分析:(1)分当点B与点G第一次重合时,当点B与点G第二次重合时,两种情况结合图形特征求解;
(2)分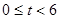 ,
,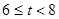 ,
,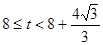 ,
,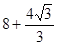
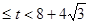 ,根据相似三角形的性质与三角形、梯形的面积公式求解即可;
,根据相似三角形的性质与三角形、梯形的面积公式求解即可;
(3)分①当旋转角为30°时,②当旋转角为75°时,这两种情况,分别画出图形,根据勾股定理及三角形的面积公式求解即可.
(1)当点B与点G第一次重合时,t=6
当点B与点G第二次重合时,t=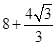 ;
;
(2)由题意得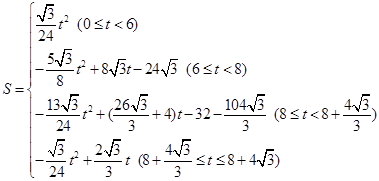 ;
;
(3)①当旋转角为30°时,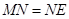
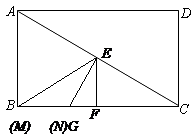
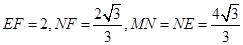
∴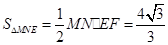 ;
;
②当旋转角为75°时,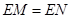
作EH⊥AB于H,MG⊥AE于G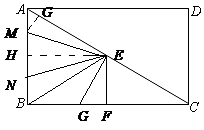
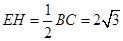 ,AH=2
,AH=2
设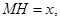
则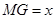 ,又∵ GE=EH=
,又∵ GE=EH=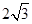
∴ 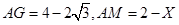
∴ 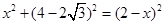
解得: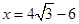
∴ 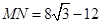
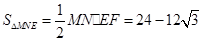
综上所述,△MNE的面积为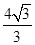 或
或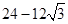 .
.
考点:动点问题的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.
19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:
 上,AH=2,连接CF.
上,AH=2,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.
已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com