
| 2 |
| x | ||
x2+a2-x
|
2x-
| ||
x2-x
|
| 1 | ||
|
| x2+a2 |
| x2+a2 |
| x2+a2 |
| x2+a2 |
| x2+a2 |
| x2+a2 |
| x | ||||
|
2x-
| ||
x(
|
| 1 | ||
|
x2-
| ||||||
x
|
x2-2x
| ||||||
x
|
(
| ||||
x
|
| ||||
x
|
| 1 |
| x |
| 2 |
| 1 | ||
1-
|
| 2 |


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
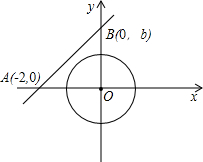 ,b)(b>0).
,b)(b>0).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•昆山市二模)如图,已知点A的坐标为(2,4),在点A处有二只蚂蚁(忽略其大小),它们同时出发,一只以每秒1个单位的速度垂直向上爬行,另一只同样以每秒1个单位的速度水平向右爬行,t秒后,它们分别到达B、C处,连接BC.若在x轴上有两点D、E,满足DB=OB,EC=OC,则
(2012•昆山市二模)如图,已知点A的坐标为(2,4),在点A处有二只蚂蚁(忽略其大小),它们同时出发,一只以每秒1个单位的速度垂直向上爬行,另一只同样以每秒1个单位的速度水平向右爬行,t秒后,它们分别到达B、C处,连接BC.若在x轴上有两点D、E,满足DB=OB,EC=OC,则查看答案和解析>>
科目:初中数学 来源: 题型:
 在Rt△ABC中,AC=6cm,BC=8cm,点P从A点出发以每秒1个单位长的速度向C点移动,点Q从C点出发以每秒2个单位长的速度向点B移动,点P、Q分别从起点同时出发,移动到某一位置所用的时间为t秒
在Rt△ABC中,AC=6cm,BC=8cm,点P从A点出发以每秒1个单位长的速度向C点移动,点Q从C点出发以每秒2个单位长的速度向点B移动,点P、Q分别从起点同时出发,移动到某一位置所用的时间为t秒查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com