
已知,抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0)
(1)求抛物线与x轴的另一个交点B的坐标;
(2)D是抛物线与y轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
(3)E是第二象限内到x轴、y轴的距离的比为5∶2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标,若不存在,请说明理由.
|
解法一: (1)依题意,抛物线对称轴为x=-2 ∵抛物线与x轴的一个交点为A(-1,0) ∴由抛物线的对称性,可得抛物线与x轴的另一个交点B的坐标为(-3,0) (2)∵抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0)
∴a(-1)2+4a(-1)+t=0 ∴t=3a ∴y=ax2+4ax+3a ∴D(0,3a) ∵梯形ABCD中,AB∥CD 且点C在抛物线y=ax2+4ax+3a上,∴C(-4,3a) ∴AB=2,CD=4 ∵梯形ABCD的面积为9 ∴ ∴ ∴a=±1 ∴所求抛物线的解析式为y=x2+4x+3或y=-x2-4x-3 (3)设点E坐标为(xO,yO)
依题意,x0<0,y0>0,且 ∴y0=- 设点E在抛物线y=x2+4x+3上, ∴y0= 解方程组 得
∵点E与A在对称轴x=-2的同侧 ∴点E坐你为(- 设在抛物线的对称轴x=-2上存在一点P,使△APE的周长最小. ∵AE长为定值 ∴要使△APE的周长最小,只须PA+PE最小. ∵点A关于对称轴x=-2的对称点是B(-3,0) ∵由几何知识可知,P是直线BE与对称轴x=-2的交点. 设过点E、B的直线的解析式为y=mx+n, ∴ 解得 把x=-2代入上式,得y= ∴点P坐标为(-2, 设点E在抛物线y=-x2-4x-3上, ∴y0=-x02-4x0-3 解方程组 消去y0,得 ∵Δ<0 ∴此方程无实数根 综上,在抛物线的对称轴上存在点P. 解法二: (1)∵抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0) ∴a(-1)2+4a(-1)+t=0 ∴t=3a ∴y=ax2+4ax+3a 令y=0,即ax2+4ax+3a=0, 解得:x1=-1,x2=-3 ∴抛物线与x轴的另一个交点B的坐标为(-3,0) (2)由y=ax2+4ax+3a,得D(0,3a) ∴梯形ABCD中,AB∥CD 且点C在抛物线y=ax2+4ax+3a上 ∴C(-4,3a) ∴AB=2,CD=4 ∵梯形ABCD的面积为9 ∴ 解得OD=3 ∴|3a|=3 ∴a=±1 ∴所求抛物线的解析式为y=x2+4x+3或y=-x2-4x-3 (3)同解法一得,P是直线BE与对称轴x=-2的交点. 如图,过点E作EQ⊥x轴于点Q
设对称轴与x轴的交点为F 由PF∥EQ, 可得 ∴ ∴PF= ∴点P坐标为(-2, 以下同解法一. |
|
有关二次曲线和二次方程的问题蕴含很多知识点,有较大的命题空间,所以一直是各地中考命题的热点.这类问题的叙述往往较长,先给出一些总的前提条件,而后一般给出2~3个小问题,其中每个小问题再给出几个针对这个问题的条件.本题第(1)小题可以根据抛物线的对称性求得,亦可令y=0解出二次方程的根,即为抛物线与x轴的交点坐标.第(2)小问利用梯形ABCD的面积,求出a的值,进而求得抛物线的解析式.第(3)小问是一道结论探索性问题,这类问题的叙述形式往往叙述为“若存在,请求出,若不存在,请说明理由”.通常的解法是,按求解题去做,若遇到不可逾越的困难或矛盾,再设法从“不存在”方面去考虑.求本小题的关键在于通过图形的分析得到直线BE的解析式,由此确定P点坐标,使问题得到解决. |


科目:初中数学 来源: 题型:
已知抛物线y=ax 2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上, 求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连结BD,若点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线y=ax![]() +bx+c与
+bx+c与![]() 轴交于
轴交于![]() 两点,若
两点,若![]() 两点的横坐标分别是一元二次方程
两点的横坐标分别是一元二次方程 的两个实数根,与
的两个实数根,与![]() 轴交于点
轴交于点![]() (0,3),
(0,3),
1.(1)求抛物线的解析式;
2.(2)在此抛物线上求点![]() ,使
,使![]() .
.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京师大附中九年级上学期期中考试数学卷 题型:解答题
已知抛物线y=ax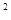 +bx+c与
+bx+c与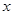 轴交于
轴交于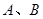 两点,若
两点,若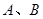 两点的横坐标分别是一元二次方程
两点的横坐标分别是一元二次方程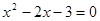 的两个实数根,与
的两个实数根,与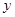 轴交于点
轴交于点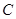 (0,3),
(0,3),
1.(1)求抛物线的解析式;
2.(2)在此抛物线上求点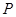 ,使
,使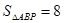 .
.
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京师大附中九年级第一学期期中考试数学卷 题型:解答题
已知抛物线y=ax +bx+c与
+bx+c与 轴交于
轴交于 两点,若
两点,若 两点的横坐标分别是一元二次方程
两点的横坐标分别是一元二次方程 的两个实数根,与
的两个实数根,与 轴交于点
轴交于点 (0,3),
(0,3),
1.(1)求抛物线的解析式;
2.(2)在此抛物线上求点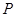 ,使
,使 .
.
查看答案和解析>>
科目:初中数学 来源:2012届湖南省九年级下学期第一次月考考试数学卷 题型:选择题
.(13分)已知抛物线y=ax 2+bx+c经过O(0,0),A(4,0),B(3,)三点,连接AB,过点B作BC∥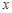 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
(1)求抛物线的解析式;
(2)记△EFA的面积为S,求S关于t的函数关系式,并求S的最大值,指出此时△EFA的形状;
 (3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
(3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com