
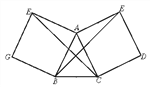
【题目】如图4,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.
求证:(1)EB=FC.(2)EB⊥FC.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据正方形的性质可得AB=AF,AC=AE,∠BAF=∠CAE=90°,然后求出∠BAE=∠CAF,再利用“边角边”证明△ABE和△AFC全等,根据全等三角形对应边相等可得EB=CF;
(2)根据全等三角形对应角相等可得∠AEB=∠ACF,连接CE,设EB、CF相交于O,然后求出∠OEC+∠OCE=90°,再求出∠COE=90°,然后根据垂直的定义即可得证.
试题解析:(1)∵四边形ACDE、BAFG都是正方形,
∴AB=AF,AC=AE,∠BAF=∠CAE=90°,
∴∠BAF+∠BAC=∠CAE+∠BAC,
即∠BAE=∠CAF,
在△ABE和△AFC中, 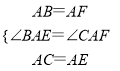 ,∴△ABE≌△AFC(SAS),
,∴△ABE≌△AFC(SAS),
∴EB=FC;
(2)∵△ABE≌△AFC,
∴∠AEB=∠ACF,
连接CE,设EB、CF相交于O,
则∠OEC+∠OCE=∠OEC+∠ACE+∠BEA=∠ACE+∠AEC=90°,
在△OCE中,∠COE=180°-(∠OEC+∠OCE)=180°-90°=90°,
∴EB⊥FC.



科目:初中数学 来源: 题型:
【题目】地表以下岩层的温度T(℃)随着所处的深度h(km)的变化而变化,T与h之间在一定范围内近似地成一次函数关系.
(1)根据下表,求T(℃)与h(km)之间的函数关系式;
温度T(℃) | … | 90 | 160 | 300 | … |
深度h(km) | … | 2 | 4 | 8 | … |
(2)当岩层温度达到1770℃时,岩层所处的深度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;

(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( ) 
A.AC=BD
B.∠CAB=∠DBA
C.∠C=∠D
D.BC=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )

A. 正方形 B. 菱形 C. 矩形 D. 无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com