
| 1 |
| 2 |
| 1 |
| 2 |
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,是2002年8月北京第24届国际数学家大会会标我国古代的数学家赵爽为证明勾股定理所作的“弦图”,它由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的积等于( )
如图,是2002年8月北京第24届国际数学家大会会标我国古代的数学家赵爽为证明勾股定理所作的“弦图”,它由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的积等于( )| A、12 | ||
B、2
| ||
| C、24 | ||
| D、10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是2002年北京第24届国际数学家大会会标,它由4个全等的直角三角形拼合而成,若图中大、小正方形的面积分别为13和1,则直角三角形的较长直角边长为
如图是2002年北京第24届国际数学家大会会标,它由4个全等的直角三角形拼合而成,若图中大、小正方形的面积分别为13和1,则直角三角形的较长直角边长为查看答案和解析>>
科目:初中数学 来源: 题型:解答题
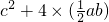 ,即
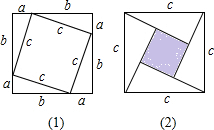
,即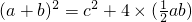 ,由此推导出一个重要的结论:a2+b2=c2,这个重要的结论就是著名的“勾股定理”.请你用两种方法求图(2)的大正方形面积,并验证勾股定理(其中四个直角三角形的较小的直角边长都为a,较大的直角边长都为b,斜边长都为c).
,由此推导出一个重要的结论:a2+b2=c2,这个重要的结论就是著名的“勾股定理”.请你用两种方法求图(2)的大正方形面积,并验证勾股定理(其中四个直角三角形的较小的直角边长都为a,较大的直角边长都为b,斜边长都为c).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com