
 如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.
如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.| BP |
| PM |
| NQ |
| QB |
 |
| BC |
| 1 |
| 4 |
| BP |
| MP |
| NQ |
| BQ |
| 1 |
| 2 |
| KQ |
| MP |
| NQ |
| KP |
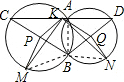 证明:①如图:连接AB,BM,BN,
证明:①如图:连接AB,BM,BN, |
| BC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BP |
| MP |
| NQ |
| BQ |
| 1 |
| 2 |
| KQ |
| MP |
| NQ |
| KP |
| 1 |
| 4 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:同步轻松练习 九年级 数学 上 题型:047
如图,半径不等的⊙O1,⊙O2外离,线段O1O2分别交⊙O1,⊙O2于点A,B,MN为两圆的公切线,分别切⊙O1,⊙O2于点M,N,连接MA,NB.请判断∠AMN与∠BNM的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:044
如图所示,两等圆⊙O1、⊙O2相交于A、B两点,且两圆互过圆心,过B作任一直线,分别交⊙O1、⊙O2于C、D两点,连接AC、AD.

(1)试猜想△ACD的形状,并给出证明;
(2)若已知条件中两圆不一定互相过圆心,试猜想三角形的形状是怎样的;
(3)若⊙O1和⊙O2是两个不等的圆,半径分别为R和r,那么(2)中的猜想还成立吗?若成立给出证明;若不成立,那么AC和AD的长与两圆的半径有什么关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.
如图,半径不等的两圆相交于A、B两点,线段CD经过点A,且分别交两于C、D两点,连接BC、CD,设P、Q、K分别是BC、BD、CD中点M、N分别是弧BC和弧BD的中点.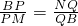 ;②△KPM∽△NQK.
;②△KPM∽△NQK.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com