
| A. | 2x2-4x+2=0 | B. | x2+2x=-1 | C. | 3x2+3x+1=0 | D. | x2+2x=1 |
分析 分别求出各个一元二次方程的根的判别式的值,进而作出判断.
解答 解:A、2x2-4x+2=0,△=16-4×2×2=0,方程有两个相等实数根,此选项错误;
B、x2+2x=-1,△=4-4×1×1=0,方程有两个相等实数根,此选项错误;
C、3x2+3x+1=0,△=9-4×3×1=-3,方程没有实数根,此选项错误;
D、x2+2x=1,△=4-4×1×(-1)=8>0,方程有两个不相等的实数根,此选项正确;
故选D.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.


科目:初中数学 来源: 题型:解答题
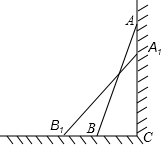 小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com