3
分析:先根据根与系数的关系可得x
1+x
2=-a,x
1x
2=b,进而分别求出x
13+x
23与x
12+x
22的值,根据已知条件x
13+x
23=x
12+x
22=x
1+x
2,于是-a
3+3ab=a
2-2b=-a,分情况讨论:①当a=0,易求b=0;②当a≠0,从等式-a
3+3ab=a
2-2b=-a入手可得a
2-3b=1①与a
2+a-2b=0②,①-②,可得a+b=-1,那么b=-a-1,再把b的值代入②,可得a
2+3a+2=0,解得a=-1或a=-2,从而可得b=0或b=1,进而可得a、b的三组数值:

或

或

,代入x
1+x
2=-a,x
1x
2=b中,可求出相应的x
1、x
2的3组数值.
解答:根据题意,得
x
1+x
2=-a,x
1x
2=b,
∵x
13+x
23=(x
1+x
2)[(x
1+x
2)
2-3x
1x
2],
∴x
13+x
23=-a(a
2-3b)=-a
3+3ab,
x
12+x
22=a
2-2b,
∵x
13+x
23=x
12+x
22=x
1+x
2,
∴-a
3+3ab=a
2-2b=-a,
(1)若a=0,则b=0;
(2)若a≠0,那么
-a(a
2-3b)=-a,
于是a
2-3b=1①,
由于a
2-2b=-a,
所以a
2+a-2b=0②,
①-②,得
a+b=-1,
于是b=-a-1,
把b=-a-1代入②,得
a
2+a-2(-a-1)=0,
化简,得
a
2+3a+2=0,
解得a=-1或a=-2,
于是b=0或b=1,
∴

或

或

,
与之对应的两根分别是

或

或

.
故答案是3.
点评:本题考查了根与系数的关系、解一元二次方程,解题的关键是要注意分情况讨论.

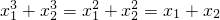 ,则我们就称这样的两个根(x1,x2)为一组“黄金根”,则这样的“黄金根”共有________组.(参考公式:a3+b3=(a+b)[(a+b)2-3ab])
,则我们就称这样的两个根(x1,x2)为一组“黄金根”,则这样的“黄金根”共有________组.(参考公式:a3+b3=(a+b)[(a+b)2-3ab]) 或
或 或
或 ,代入x1+x2=-a,x1x2=b中,可求出相应的x1、x2的3组数值.
,代入x1+x2=-a,x1x2=b中,可求出相应的x1、x2的3组数值. 或
或 或
或 ,
, 或
或 或
或 .
.
