
 →线段DB;图2:的路线:线段AE→
→线段DB;图2:的路线:线段AE→ →线段FB(其中E、F为切点)
→线段FB(其中E、F为切点) 
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
 |
| CD |
 |
| EF |
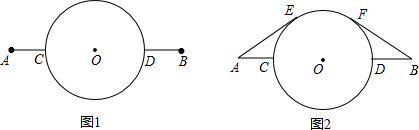
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知公路上有A、B、C三个汽车站,A、C两站相距280km,一辆汽车上午8点从离A站40km的P地出发,以80km/h的速度向C站匀速行驶,到达C站休息半小时后,再以相同的速度沿原路匀速返回A站.
如图,已知公路上有A、B、C三个汽车站,A、C两站相距280km,一辆汽车上午8点从离A站40km的P地出发,以80km/h的速度向C站匀速行驶,到达C站休息半小时后,再以相同的速度沿原路匀速返回A站.查看答案和解析>>
科目:初中数学 来源: 题型:044
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为![]() 为最短路线(其中
为最短路线(其中 ,
, 都与⊙O相切).你能计算出这段公路的长度吗?(结果精确到0.1km)
都与⊙O相切).你能计算出这段公路的长度吗?(结果精确到0.1km)

查看答案和解析>>
科目:初中数学 来源:2004年新疆建设兵团中考数学试卷(解析版) 题型:解答题
 →线段DB;图2:的路线:线段AE→
→线段DB;图2:的路线:线段AE→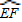 →线段FB(其中E、F为切点)
→线段FB(其中E、F为切点) 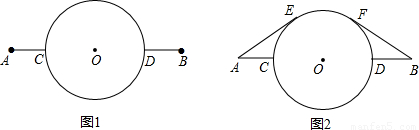
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com