A
分析:首先过△ABC顶点A作BC边上的高AD,由已知得BD=CD,再由两个直角三角形运用勾股定理推出即P
1=AQ
12+Q
1B•Q
1C=AB
2=16,同理同理:P
2=16,P
3=16,…,P
n=16,从而求解.
解答:
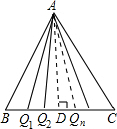
解:过△ABC顶点A作BC边上的高AD,
∵AB=AC,
∴BD=CD,
在Rt△ADQ
1中,由勾股定理得:
AQ
12=AD
2+Q
1D
2,
在Rt△ABD中,由勾股定理得:
AD
2=AB
2-BD
2,
所以AQ
12+Q
1B•Q
1C
=AD
2+Q
1D
2+Q
1B•Q
1C
=(AB
2-BD
2)+Q
1D
2+Q
1B•Q
1C
=AB
2-BD
2+Q
1D
2+(BD-Q
1D)(CD+Q
1D)
=AB
2-BD
2+Q
1D
2+(BD-Q
1D)(BD+Q
1D)
=AB
2-BD
2+Q
1D
2+BD
2-Q
1D
2=AB
2=4
2=16,
即P
1=16,
同理:P
2=16,P
3=16,…,P
n=16,
所以P
1+P
2+P
3+…+P
n=16+16+16+…+16=16n,
故选:A.
点评:此题考查的知识点是勾股定理,关键是由已知等腰三角形作底边的高,得两直角三角形,运用勾股定理及等腰三角形的性质推出AQ
12+Q
1B•Q
1C=AB
2.

 解:过△ABC顶点A作BC边上的高AD,
解:过△ABC顶点A作BC边上的高AD,

 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°, ,连接AO、BE、DC.
,连接AO、BE、DC.