解:(1)AB=AE,AB⊥AE;
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合),
理由如下:
∵AC⊥BC,DF⊥EF,B、F、C、E共线,
∴∠ACB=∠ACE=∠DFE=90°,
又∵AC=BC,DF=EF,
∴∠DEF=∠D=45°,
在△CEG中,∵∠ACE=90°,
∴∠CGE+∠DEF=90°
∴∠CGE=∠DEF=45°,
∴CG=CE,
在△BCG和△ACE中,
∵
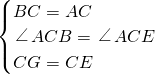
,
∴△BCG≌△ACE(SAS),
∴将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合).
分析:(1)根据题意,BC=AC=DF=EF,且AC⊥BC,可知△ABC,△DEF为等腰直角三角形,得出结论;
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合.已知BC=AC,由(1)可知∠DEF=45°,可知△CEG为等腰直角三角形,则CG=CE,利用“SAS”证明△BCG≌△ACE,得出结论.
点评:本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定与性质.关键是熟练运用等腰直角三角形的性质解题.


 ,
,

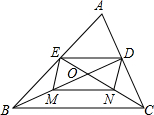 如图,△ABC的边AC、AB上的中线BD、CE相交于点O,M、N分别是BO、CO的中点,顺次连接点D、E、M、N.
如图,△ABC的边AC、AB上的中线BD、CE相交于点O,M、N分别是BO、CO的中点,顺次连接点D、E、M、N.