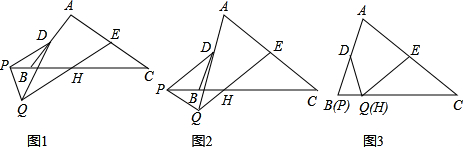
解:结论:EH=

AC.
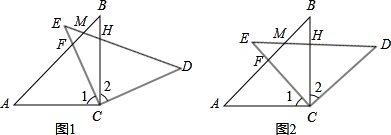
证明:取BC边中点F,连接DE、DF.
∵D、E、F分别是边AB、AC、BC的中点.
∴DE∥BC且DE=

BC,
DF∥AC且DF=

AC,
EC=

AC∴四边形DFCE是平行四边形.
∴∠EDF=∠C.
∵∠C=∠PDQ,∴∠PDQ=∠EDF,∴∠PDF=∠QDE.
又∵AC=kBC,∴DF=kDE.
∵DP=kDQ,∴
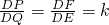
.
∴△PDF∽△QDE.
∴∠DEQ=∠DFP.
又∵DE∥BC,DF∥AC,∴∠DEQ=∠EHC,∠DFP=∠C.
∴∠C=∠EHC.
∴EH=EC.
∴EH=

AC.
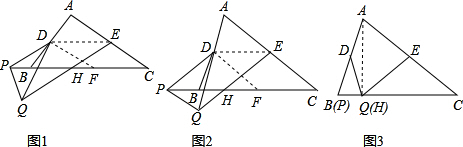
选图2.结论:EH=

AC.
证明:取BC边中点F,连接DE、DF.
∵D、E、F分别是边AB、AC、BC的中点,
∴DE∥BC且DE=

BC,DF∥AC且DF=

AC,
EC=

AC,∴四边形DFCE是平行四边形.
∴∠EDF=∠C.
∵∠C=∠PDQ,∴∠PDQ=∠EDF,∴∠PDF=∠QDE.
又∵AC=BC,∴DE=DF,∵PD=QD,∴△PDF≌△QDE.
∴∠DEQ=∠DFP.
∵DE∥BC,DF∥AC,∴∠DEQ=∠EHC,∠DFP=∠C.
∴∠C=∠EHC
∴EH=EC.
∴EH=

AC.
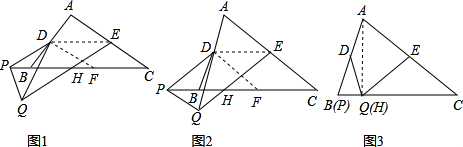
选图3.结论:EH=

AC.
证明:连接AH.
∵D是AB中点,∴DA=DB.
∵AC=kBC,DP=kDQ,
∴
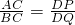
=k,
又∵∠C=∠PDQ,
∴△ACB∽△PDQ,
∴∠ABC=∠PQD,
∴DB=DQ,
∴DQ=DP=AD,
∵∠DBQ+∠DQB+∠DQA+∠DAQ=180°,
∴∠AQB=90°,
∴AH⊥BC.
又∵E是AC中点,
∴HE=

AC.
分析:(1)取BC中点F,连接DE,DF.利用三角形中位线性质可知四边形DFCE是平行四边形,由已知中角的相等,利用等量相加和相等,可得∠PDF=∠QDE,DF∥AC,可得
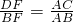
,即DF=kDE(DE=BF=

BC),可证出△PDF∽△QDE.就有∠DFB=∠DEQ,又DE,BC平行可得∠DEQ=∠EHC,那么等量代换就有∠EHC=∠DFB=∠C,因此得证.
(2)和(1)的证法相同.
(3)连接AQ,利用已知条件可证出△DPQ∽△ACB,那么就有∠ABC=∠BAC,且∠DBQ=∠DQB,那么DB=DQ.能判定△ABQ是直角三角形,同样,△AQC也是直角三角形,HE是斜边上的高,所以就有EH=

AC.
点评:本题利用了三角形中位线的判定和性质,平行四边形的判定和性质,相似三角形的判定和性质等知识.

 AC.
AC. 证明:取BC边中点F,连接DE、DF.
证明:取BC边中点F,连接DE、DF. BC,
BC, AC,
AC, AC∴四边形DFCE是平行四边形.
AC∴四边形DFCE是平行四边形.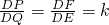 .
. AC.
AC. AC.
AC. BC,DF∥AC且DF=
BC,DF∥AC且DF= AC,
AC, AC,∴四边形DFCE是平行四边形.
AC,∴四边形DFCE是平行四边形. AC.
AC. 选图3.结论:EH=
选图3.结论:EH= AC.
AC.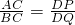 =k,
=k, AC.
AC.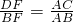 ,即DF=kDE(DE=BF=
,即DF=kDE(DE=BF= BC),可证出△PDF∽△QDE.就有∠DFB=∠DEQ,又DE,BC平行可得∠DEQ=∠EHC,那么等量代换就有∠EHC=∠DFB=∠C,因此得证.
BC),可证出△PDF∽△QDE.就有∠DFB=∠DEQ,又DE,BC平行可得∠DEQ=∠EHC,那么等量代换就有∠EHC=∠DFB=∠C,因此得证. AC.
AC.