
已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.
100°
【解析】
试题分析:设点P关于OM、ON对称点分别为P′、P″,当点A、B在P′P″上时,△PAB周长为PA+AB+BP=P′P″,此时周长最小.根据轴对称的性质,可求出∠APB的度数.
分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A、B,连接PA、PB,此时△PAB周长的最小值等于P′P″.
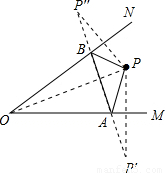
由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,
∴∠P′OP″=2∠MON=2×40°=80°,
∴∠OP′P″=∠OP″P′=(180°-80°)÷2=50°,
又∵∠BPO=∠OP″B=50°,∠APO=∠AP′O=50°,
∴∠APB=∠APO+∠BPO=100°.
考点:本题主要考查了轴对称--最短路线问题
点评:根据两点之间线段最短的知识画出图形是解答此类题目的关键.


科目:初中数学 来源: 题型:
 22、如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.(先作图,再计算)
22、如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.(先作图,再计算)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.(先作图,再计算)
如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.(先作图,再计算)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com