
如下图,在矩形ABCD中,AB=4,BC=3,O是对角线BD的中点,点P在边AB上,联结PO并延长,交边CD于点E,交边BC的延长线于点Q.

(1)求证:OP=OE;
(2)设BP=x,CQ=y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)试判断△CQE能否成为等腰直角三角形,如果能,请求出x的值;如果不能,请说明理由.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
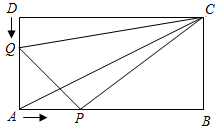 如下图,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6)那么:
如下图,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6)那么:查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川省资阳市安岳县自治乡九义校九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年山东省泰安市新泰市中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年甘肃省兰州市中考数学模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《图形的相似》(03)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com