
如图:在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,AB=10,AC=6,求D到AB的距离.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点 B重合),分别连接ED,EC,可以把
B重合),分别连接ED,EC,可以把
四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上
的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形AB CD的边AB上的相似点,并说明理由;
CD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方
形的边长为1 )的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
现有三个自愿献血者,两人血型为O型,一人血型为A型.若在三人中随意挑选一人献血,两年以后又从此三人中随意挑选一人献血,试求两次所献血的血型均为O型的概率(要求:用列表或画树状图的方法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
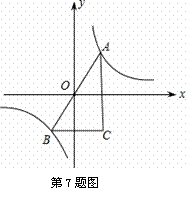
如图,A,B是反比例函数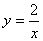 的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC
的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC 的面积记为S,则
的面积记为S,则
A.S = 2 B. 2<S<4 C.S = 4 D.S>4
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等边△AMN,联结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.联结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
 xkb1.com
xkb1.com
查看答案和解析>>
科目:初中数学 来源: 题型:
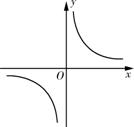
反比例函数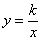 的图象如图所示,以下结论:①常数
的图象如图所示,以下结论:①常数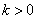 ;②当
;②当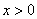 时,函数值
时,函数值 ;③
;③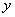 随
随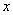 的增大而减小;④若点
的增大而减小;④若点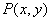 在此函数图象上,则点
在此函数图象上,则点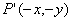 也在此函数图象上.其中正确的是 ( )
也在此函数图象上.其中正确的是 ( )
A.①②③④ B.①②③  C.①②④ D.②③④
C.①②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
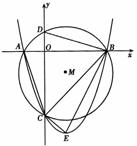
如图,在平面直角坐标系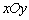 中,以点
中,以点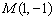 为圆心,以
为圆心,以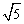 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经
的图象经
过点A、B、C,顶点为E.
(1)求此二次函数的表达式;
(2)设∠DBC=a,∠CBE=b,求sin(a-b)的值;
(3)坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
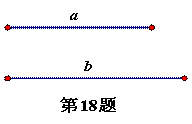
古希腊数学家丢番图(公元250年前后)在《算术》中就提到了一元二次方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解。在欧几里得的《几何原本》中,形如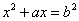 (a>0,b>0)的方程的图解法是:以
(a>0,b>0)的方程的图解法是:以 和b为两直角边做Rt△ABC,再在斜边上截取BD=
和b为两直角边做Rt△ABC,再在斜边上截取BD= ,则AD的长就是所求方程的解。
,则AD的长就是所求方程的解。
(1)请利用所给的线段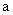 和线段b,作出方程的解。
和线段b,作出方程的解。
(2)说说上述求法的不足之处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com