
 如图点A,点B是反比例函数
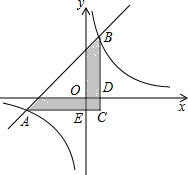
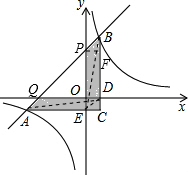
如图点A,点B是反比例函数 上两点,过这两点的直线与x轴的夹角为45度,与y轴的交点为(0,2),作AC∥x轴,AC⊥BC于点C,
上两点,过这两点的直线与x轴的夹角为45度,与y轴的交点为(0,2),作AC∥x轴,AC⊥BC于点C,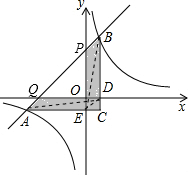 直线AB交两坐标轴分别为P点和Q点,如图,
直线AB交两坐标轴分别为P点和Q点,如图, ),B(n,
),B(n, ),直线AB的解析式为y=ax+b,
),直线AB的解析式为y=ax+b, =ma+b,
=ma+b, =na+b,
=na+b,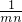 k,b=
k,b=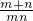 k,
k,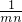 kx+
kx+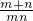 k,
k,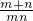 k),Q(m+n,0),
k),Q(m+n,0), (n-m)(
(n-m)( -
- )-
)- [-(m+n)]•
[-(m+n)]•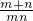 =2k;
=2k; •
• •n=
•n= k,S△ADE=
k,S△ADE= •(-m)•(-
•(-m)•(- )=
)= k,
k, ,
, -2a=2,
-2a=2, -1,
-1, +1,
+1, -1)(
-1)( +1)=1,
+1)=1, .
.
 ;一次函数:y=x+2.
;一次函数:y=x+2.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源:2011-2012学年浙江省嘉兴市桐乡三中九年级(上)期中数学试卷(解析版) 题型:填空题
 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .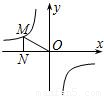
查看答案和解析>>
科目:初中数学 来源:2010-2011学年浙江省绍兴市嵊州市九年级(上)期末训练数学试卷(解析版) 题型:填空题
 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
查看答案和解析>>
科目:初中数学 来源:2013年山东省青岛市中考数学模拟试卷(二十二)(解析版) 题型:填空题
 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
查看答案和解析>>
科目:初中数学 来源:2012年广东省深圳市龙岗区中考数学调研试卷(解析版) 题型:填空题
 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com