解:(1)如图所示:∠PAQ即为所求;
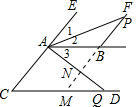
(2)AP=AQ.理由如下:
如图所示,延长PB,分别交AQ与CD于N、M点,则∠1+∠2=∠EAB,
∵∠PAQ=∠EAB,且∠2+∠3=∠PAQ,
∴∠3=∠1.
∵AB∥CD,
∴∠AQM=∠3=∠1,∠EAB=∠C.
∵BF∥EA,
∴∠APB=∠1,∠PMQ=∠C=∠EAB,
∴∠EAB=∠C=∠PAQ=∠PMQ,∠1=∠3=∠APB=∠AQM.
∵AB∥CD,AC∥BM,
∴四边形ACMB是平行四边形,
又∵AB=AC,
∴四边形ABMC是菱形.
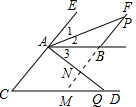
设AB=AC=CM=BM=a.
∵MN∥AC,
∴△ACQ∽△NMQ,
∴
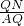
=
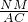
=
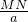
,
∴QN•a=MN•AQ ①,
∵AB∥CD,
∴△NQM∽△NAB,
∴
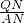
=
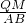
=
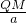
,
∴QN•a=QM•AN ②,
比较①与②,得MN•AQ=QM•AN,
∴

=
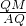
;
∵∠NQM=∠NPA,∠QNM=∠PNA,
∴△NQM∽△NPA,
∴

=
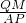
,
∴
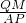
=
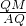
,
∴AP=AQ.
故答案为AP=AQ;
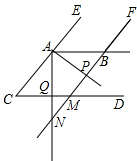
(3)(2)中的结论还成立,理由如下:
如图所示,设FB交CD于M,FB交AQ于N.
∵AC∥FN,
∴∠CAQ=∠N,
又∵∠AQC=∠NQM,
∴△ACQ∽△NMQ,
∴
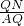
=
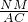
=
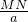
,
∴QN•a=MN•AQ,
∵AB∥CD,
∴△NQM∽△NAB,
∴
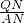
=
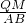
=
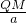
,
∴QN•a=QM•AN,
∴MN•AQ=QM•AN,
∴

=
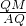
;
∵AB∥CD,
∴∠EAB=∠C,
∵∠PAQ=∠EAB,
∴∠C=∠PAQ,
∵AC∥BN,
∴∠QMN=∠C,
∴∠PAQ=∠QMN,
又∵∠N=∠N,
∴△NQM∽△NPA,
∴

=
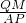
,
∴
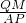
=
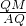
,
∴AP=AQ.
分析:(1)根据将∠EAB绕点A顺时针旋转,∠EAB的两边分别交射线BF于点P,交射线CD于点Q,得出∠EAB=∠PAQ即可;
(2)根据已知首先证明四边形ACMB是平行四边形,进而得出四边形ABMC是菱形,由△ACQ∽△NMQ,得出QN•a=MN•AQ,由△NQM∽△NAB,得出QN•a=QM•AN,则MN•AQ=QM•AN,即

=
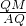
;又由△NQM∽△NPA,得出
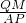
=

,进而得出AP=AQ;
(3)利用已知可得△ACQ∽△NMQ,△NQM∽△NAB,△NQM∽△NPA,进而根据相似三角形的性质得出对应边关系,进而得出AP=AQ.
点评:本题考查了作图-旋转变换,菱形的判定,相似三角形的判定与性质,有一定难度.

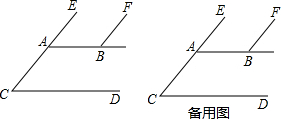

 设AB=AC=CM=BM=a.
设AB=AC=CM=BM=a.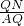 =
=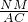 =
=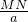 ,
,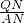 =
=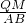 =
=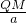 ,
, =
=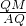 ;
; =
=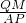 ,
,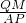 =
=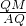 ,
, (3)(2)中的结论还成立,理由如下:
(3)(2)中的结论还成立,理由如下: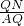 =
=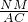 =
=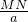 ,
,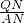 =
=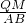 =
=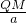 ,
, =
=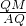 ;
; =
=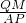 ,
,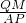 =
=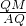 ,
, =
=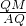 ;又由△NQM∽△NPA,得出
;又由△NQM∽△NPA,得出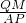 =
= ,进而得出AP=AQ;
,进而得出AP=AQ;

 如图,射线AM交一圆于点B、C,射线AN交该圆于点D、E,且
如图,射线AM交一圆于点B、C,射线AN交该圆于点D、E,且