
 (2012•利川市一模)折纸与证明---用纸折出黄金分割点:
(2012•利川市一模)折纸与证明---用纸折出黄金分割点:| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
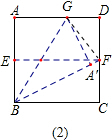 证明:如图,连接GF,设正方形ABCD的边长为1,则DF=
证明:如图,连接GF,设正方形ABCD的边长为1,则DF=| 1 |
| 2 |
| BC2+CF2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
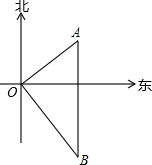 (2012•利川市二模)小明在海边观景台O处,观测到北偏东60°的A处有一艘货船,该船正向南匀速航行,10分钟后再观察时,该船已航行到O的南偏东30°,且与O相距3km的B处,如图所示.(参考数据:
(2012•利川市二模)小明在海边观景台O处,观测到北偏东60°的A处有一艘货船,该船正向南匀速航行,10分钟后再观察时,该船已航行到O的南偏东30°,且与O相距3km的B处,如图所示.(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com