
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
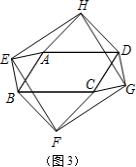 ②证明:∵△AEB和△DGC是等腰直角三角形,
②证明:∵△AEB和△DGC是等腰直角三角形,
| ||
| 2 |
| ||
| 2 |


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
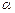 (0°<
(0°<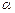 <90°),
<90°),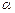 的代数式表示∠HAE= ;(1分)
的代数式表示∠HAE= ;(1分)
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省苏州张家港市第二中学八年级上学期期中考试数学卷 题型:解答题
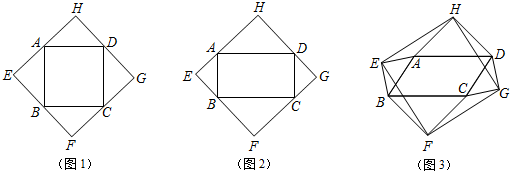
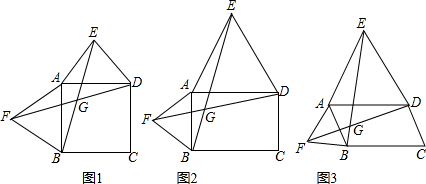
(本题10分) 以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点得四边形EFGH.如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;
【小题1】(1)如图2,当四边形ABCD为矩形时,则四边形EFGH的形状是 ;(1分)
【小题2】(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC= (0°<
(0°< <90°),
<90°),
【小题3】① 试用含 的代数式表示∠HAE= ;(1分)
的代数式表示∠HAE= ;(1分)
【小题4】② 求证:HE=HG;(4分)③ 四边形EFGH是什么四边形?并说明理由.(4分)
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省苏州张家港市八年级上学期期中考试数学卷 题型:解答题
(本题10分) 以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点得四边形EFGH.如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;
1.(1)如图2,当四边形ABCD为矩形时,则四边形EFGH的形状是 ;(1分)
2.(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC= (0°<
(0°< <90°),
<90°),
3.① 试用含 的代数式表示∠HAE=
;(1分)
的代数式表示∠HAE=
;(1分)
4.② 求证:HE=HG;(4分)③ 四边形EFGH是什么四边形?并说明理由.(4分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com