
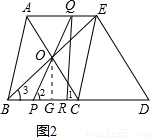
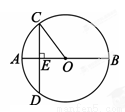
��ͼ1���ڡ�ABC�У�AB��BC��5��AC=6.��ECD�ǡ�ABC��BC����ƽ�Ƶõ��ģ����� AE.AC��BE�ཻ�ڵ�O.
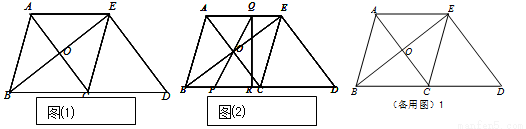
��1���ж��ı���ABCE���������ı��Σ�˵�����ɣ�
��2����ͼ2��P���߶�BC��һ���㣨ͼ2�����������B��C�غϣ�������PO���ӳ����߶�AB�ڵ�Q��QR��BD������Ϊ��R.
���ı���PQED������Ƿ����P���˶��������仯�����仯����˵�����ɣ������䣬����ı���PQED�������
�ڵ��߶�BP�ij�Ϊ��ֵʱ����PQR���BOC���ƣ�
��������
��1���ı���ABCE�����Σ�
�ߡ�ECD���ɡ�ABC��BCƽ�Ƶõ��ģ�
��EC��AB����EC=AB��
���ı���ABCE��ƽ���ı��Σ�
�֡�AB=BC��
���ı���ABCE�����Σ�
��2�����ı���PQED������������仯��
����һ����ABCE�����Σ�
��AC��BE��OC=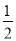 AC=3��
AC=3��
��BC=5��
��BO=4��
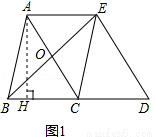
��A��AH��BD��H������ͼ1��
��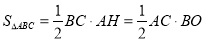 ��
��
��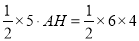 ��
��
���AH=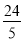 ��
��
��ߡ�AHC=��BOC=90�㣬��BCA=��BCA��
���AHC�ס�BOC��
��AH��BO=AC��BC��
��AH��4=6��5��
��AH=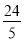 ��
��
�����εĶԳ���֪����PBO�ա�QEO��
��BP=QE��
��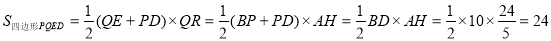
�������������εĶԳ���֪����PBO�ա�QEO��
��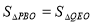 ��
��
�ߡ�ECD���ɡ�ABCƽ�Ƶõ��ģ�
��ED��AC��ED=AC=6��
�֡�BE��AC��
��BE��ED��
��
�ڷ���һ����ͼ2��
����P��BC���˶���ʹ��PQR���COB����ʱ��
�ߡ�2�ǡ�OBP����ǣ�
���2����3��
���2�����3��Ӧ��
���2���1��Ӧ��
����2=��1��
��OP=OC=3
��O��OG��BC��G����GΪPC���е㣬
���OGC�ס�BOC��
��CG��CO=CO��BC��
��CG��3=3��5��
��CG=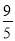 ��
��
��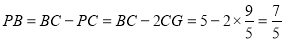 ��
��
����������ͼ3��
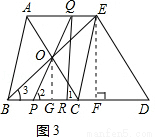
����P��BC���˶���ʹ��PQR���COB����ʱ��
�ߡ�2�ǡ�OBP����ǣ�
���2����3��
���2�����3��Ӧ��
���2���1��Ӧ��
��QR��BO=PR��OC
��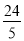 ��4=PR��3��
��4=PR��3��
��PR=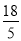 ��
��
��E��EF��BD��F����PB=x����RF=QE=PB=x��
DF=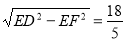 ��
��
��BD=PB+PR+RF+DF=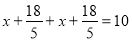 ��
��
���x=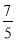 ��
��
����������ͼ4��
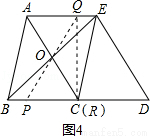
����P��BC���˶���ʹ��R��C�غϣ�
�����εĶԳ���֪��OΪPQ���е㣬
��CO��Rt��PCQб���ϵ����ߣ�
��CO=PO��
���OPC=��OCP��
��ʱ��Rt��PQR��Rt��CBO��
��PR��CO=PQ��BC��
��PR��3=6��5��
��PR=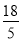
��PB=BC��PR= ��
��
��������
�����������1���ı���ABCE�����Σ���ƽ�Ƶõ��ı���ABCE��ƽ���ı��Σ���AB=BC�������Ƴ��ı���ABCE�����Σ�
��2�����ı���PQED������������仯���������ε����ʺ���֪��������������ε��������A��AH��BD��H���ٸ��������ε������ʽ�������AH�������εĶԳ���֪��PBO�ա�QEO������BP=QE�����ڿ��Եõ� ������BED�������������������ı���PQED������������仯��
������BED�������������������ı���PQED������������仯��
����ͼ2������P��BC���˶���ʹ��PQR���COB����ʱ���ߡ�2�ǡ�OBP����ǣ����2����3�����2�����3��Ӧ�����2���1��Ӧ������2=��1����OP=OC=3����O��OG��BC��G����GΪPC���е㣬��OGC�ס�BOC���������������εĶ�Ӧ�߶γɱ����������CG����PB=BC��PC=BC��2CG�����������ʽ�Ϳ������BP�ij���
���㣺���ε��ж���ȫ�������ε��ж������ʣ����������ε��ж�������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ӱ�ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��8�֣���һ���Ϊ150m2�ij����μ�����������һ�߿�ǽ��ǽ��18 m�����������������Χ�ɣ��������ʵ��ܳ�Ϊ35 m�����ij������Ϊ���٣�
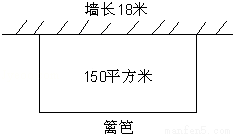
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ���꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ���½�Ϊ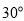 ��б�����������ˮƽ����
��б�����������ˮƽ����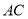 Ϊ
Ϊ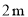 ������������������
������������������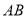 �� ��
�� ��
A��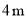 B��
B��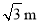 C��
C��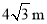 D��
D��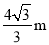
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ�����з�У���꼶��ѧ�ڵ����νο�����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ڡ�O�У���D=70�㣬��ACB=50�㣬���BAC= .
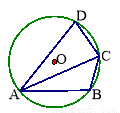
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ�����з�У���꼶��ѧ�ڵ����νο�����ѧ�Ծ��������棩 ���ͣ�ѡ����
ƽ����4���㣬���Dz���һ��ֱ���ϣ�����3������ͬһ��ֱ���ϡ�������3������Բ����������Բ�ĸ����ǣ� ��
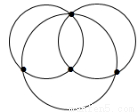
A.1�� B.2�� C.3�� D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ������СƬ�����꼶��ѧ�ڰ��ڿ�����ѧ�Ծ��������棩 ���ͣ������
����������10�֣���ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���Ҫ����A1B1C1�͡�A2B2C2��
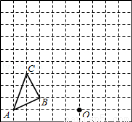
��1���ѡ�ABC������ƽ��4����λ��������ƽ��1����λ���õ���A1B1C1��
��2����ͼ�е�OΪλ�����ģ�����A1B1C1��λ�Ʊ任�ҷŴ�ԭ�����������õ���A2B2C2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ������СƬ�����꼶��ѧ�ڰ��ڿ�����ѧ�Ծ��������棩 ���ͣ������
��֪���ε��ܳ�Ϊ24cm��һ���Խ��߳�Ϊ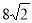 cm��������ε����Ϊ_________��
cm��������ε����Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱����ƽ�������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
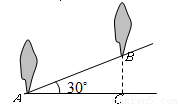
��ͼ��һ�κ�����ͼ���� �ᡢ
�ᡢ ��ֱ��ཻ��A��B���㣬���뷴����������ͼ���ڵڶ������ڵ�C�������A������Ϊ
��ֱ��ཻ��A��B���㣬���뷴����������ͼ���ڵڶ������ڵ�C�������A������Ϊ ��OA=2OB���� B��AC���е㣮
��OA=2OB���� B��AC���е㣮

��1�����C�����ꣻ
��2����һ�κ����ͷ����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱���о��꼶��ѧ�����м����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��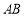 Ϊ��
Ϊ��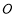 ��ֱ������
��ֱ������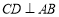 ������Ϊ��
��������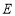 ������
������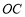 ����
����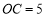 ��
��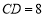 ����
����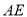 �ij��� ��
�ij��� ��
A��5 B��4 C��3 D��2
B��4 C��3 D��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com