
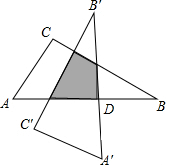
 如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )
如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )| A. | 6 | B. | 9 | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
分析 如图,先计算出AB=2AC=12,则BD=6,再根据旋转的性质得B′D′=BD=6,则在Rt△BDM中可计算出DM=2$\sqrt{3}$,BM=2MD=4$\sqrt{3}$,所以B′M=B′D-DM=6-2$\sqrt{3}$,接着在Rt△B′MN中计算出MN=$\frac{1}{2}$B′M=3-$\sqrt{3}$,所以BN=3+3$\sqrt{3}$,在Rt△BNG中计算NG=$\frac{\sqrt{3}}{3}$BN=3+$\sqrt{3}$,然后利用S阴影部分=S△BNG-S△BDM进行计算即可.
解答 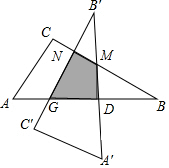 解:如图,
解:如图,
∵∠C=90°,∠A=60°,AC=6,
∴AB=2AC=12,
∵点D为AB的中点,
∴BD=6,
∵△ABC绕点D逆时针方向旋转90°得到Rt△A′B′C′,
∴B′D′=BD=6,
在Rt△BDM中,∵∠B=30°,
∴DM=$\frac{\sqrt{3}}{3}$BD=2$\sqrt{3}$,BM=2MD=4$\sqrt{3}$,
∴B′M=B′D-DM=6-2$\sqrt{3}$,
在Rt△B′MN中,MN=$\frac{1}{2}$B′M=3-$\sqrt{3}$,
∴BN=3-$\sqrt{3}$+4$\sqrt{3}$=3+3$\sqrt{3}$,
在Rt△BNG中,NG=$\frac{\sqrt{3}}{3}$BN=3+$\sqrt{3}$,
∴S阴影部分=S△BNG-S△BDM=$\frac{1}{2}$•(3+$\sqrt{3}$)•(3+3$\sqrt{3}$)-$\frac{1}{2}$•2$\sqrt{3}$•6=9.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系和三角形面积公式.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )
如图,四边形ABCD中DC∥AB,将四边形沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( )| A. | 66° | B. | 104° | C. | 114° | D. | 124° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
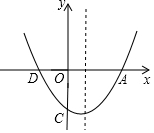 如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).
如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
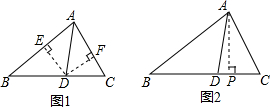 让我们来共同探究“三角形的角平分线”的特殊性质:
让我们来共同探究“三角形的角平分线”的特殊性质:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
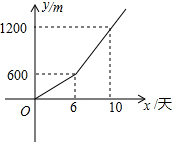 (1)在学习一次函数的图象时,我们根据函数图象的定义,按画函数图象的基本步骤,画出一次函数的图象,请您按画函数图象的基本步骤画出函数y=2x+4的图象.
(1)在学习一次函数的图象时,我们根据函数图象的定义,按画函数图象的基本步骤,画出一次函数的图象,请您按画函数图象的基本步骤画出函数y=2x+4的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com