解:(1)由题意得:2008年住房单价为
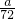
,2009年住房单价为
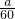
,
所以2009年住房单价涨幅是(
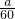
-
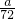
)÷
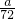
=20%;
(2)设2009年装修费上涨的百分数为x,2008年购买这套住房费用为b元,
那么2010年购房费和装修费分别为:b(1+20%)
2和25%b(1+x)
2,
(说明:如果缺少以上两步,但只要在方程中出现了式子25%a(1+x)
2 和式子b(1+20%)
2,无论方程是否正确,都可以各评1分)
列方程得:b(1+20%)
2+25%b(1+x)
2=(b+25%b)×(1+36%),
化简得:(1+x)
2=1.04,
解得:x
1≈0.02=2%,x
2≈-2.02(负根舍去).
答:2009年装修费上涨的百分数是2%.
分析:(1)分别表示出2008年与2009年的住房单价,利用两年的房价差值除以2009年的住房单价,进而得出2009年住房单价涨幅;
(2)设2009年装修费上涨的百分数为x,2008年购买这套住房费用为b元,得出2010年购房费和装修费分别为:b(1+20%)
2和25%b(1+x)
2,进而利用2010年所需的购房费与装修费之和比2008年支出的这两项费用之和还多36%,得出等式方程求出即可.
点评:此题主要考查了一元二次方程的应用,以及增长率问题,正确表示出2010年购房费和装修费用是解决问题的关键.

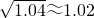 )
)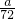 ,2009年住房单价为
,2009年住房单价为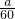 ,
,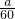 -
-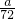 )÷
)÷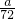 =20%;
=20%;

 阅读快车系列答案
阅读快车系列答案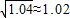 )
)