
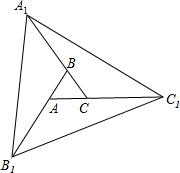
 如图,把面积为1的等边△ABC的三边分别向外延长m倍,得到△A1B1C1,那么△A1B1C1的面积是3m2+3m+1(用含m的式子表示)
如图,把面积为1的等边△ABC的三边分别向外延长m倍,得到△A1B1C1,那么△A1B1C1的面积是3m2+3m+1(用含m的式子表示) 分析 连接AB1,BC1,CA1,根据等底等高的三角形的面积相等求出△ABB1,△A1AB1的面积,从而求出△A1BB1的面积,同理可求△B1CC1的面积,△A1AC1的面积,然后相加即可得解.
解答 解: 如图,连接AA1,B1C2,BC1,如图所示:
如图,连接AA1,B1C2,BC1,如图所示:
∵把面积为1的等边△ABC的三边分别向外延长m倍,
∴△A1 AB的面积=△BC2C1 的面积=△AB1C2的面积=m×1=m,
同理:△A1B1 A的面积=△B1 C1 C2 的面积=△A1 BC1 的面积=m×m=m2,
∴△A1B1C1的面积=3m2+3m+1;
故答案为:3m2+3m+1.
点评 本题考查了三角形的面积,主要利用了等底等高的三角形的面积相等,作辅助线把三角形进行分割是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求完成以下问题的解答过程:
按要求完成以下问题的解答过程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com